By capturing miniscule details in complex geometries, high-order meshes increase the accuracy of scientific simulations. But these highly discretized domains require significant computing power, so researchers often seek more effective numerical methods for improving finite element solution performance.

For example, one major challenge involves efficiently locating a given point in the mesh’s physical space and evaluating the partial differential equation (PDE) solution there. Solving this problem is essential for tasks such as probing simulations to monitor a quantity of interest (e.g., drag forces along an airplane wing) and coupling physics across different simulations.

“The capability we present has been a key enabler of simulation campaigns on massive supercomputers to study shock-driven flows, perform structural design optimization, and understand sediment transport in rivers,” says Ketan Mittal, computational mathematician and lead author of a new paper in Computers and Fluids. “General Field Evaluation in High-Order Meshes on GPUs” describes an innovative way to evaluate PDE solutions at any location in a mesh and adapts the method to graphics processing unit (GPU)–based computing architectures.

Mittal’s co-authors are Aditya Parik (former LLNL intern studying at Utah State University), Som Dutta (also from Utah State), Paul Fischer (University of Illinois at Urbana-Champaign and Argonne National Laboratory), Tzanio Kolev (LLNL), and James Lottes (Google Research).

Compounding Challenges

A mesh consists of elements that are distributed across a supercomputer’s processors for parallel computation. According to the Message Passing Interface (MPI) standard, each central processing unit (CPU) core receives a unique identifier known as an MPI rank, which is used to assign each element to the CPU(s) responsible for managing the associated workload and simulation data.

Modern supercomputers often pair CPUs with GPUs to significantly accelerate the desired computation. To query the PDE solution at a specific physical location over the mesh, the simulation first has to determine where the point is located—i.e., on which element and which MPI rank—and then compute the local coordinates corresponding to that point inside the element.

Finding the assigned MPI rank and its corresponding element is challenging, especially for millions of points distributed across as many MPI ranks. “We have not seen a robust and scalable solution to this problem in the literature, especially for parallel computations,” Mittal points out.

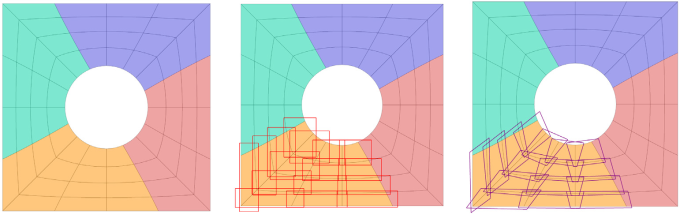
The team leverages a sequence of maps and bounding boxes to narrow down the list of MPI ranks and elements that may overlap a given point (Figure 1). Then, the technique searches these candidate elements by solving an optimization problem, thus determining which element overlaps the point along with the local coordinates inside that element.

Figure 1: A high-order unstructured mesh is mapped to four MPI ranks shown in four colors (left). The team’s technique of quickly determining which elements may overlap a point relies on using axis-aligned (center), and oriented bounding boxes (right). (Click to enlarge.)

“These maps and bounding boxes help find the overlapping elements for millions of points in less than a second,” states Mittal. The PDE solution is then trivial to evaluate using the simulation data: The mesh only needs to be pre-processed once to compute the maps and boxes, and this information can be re-used during the simulation.

Scaling on GPUs

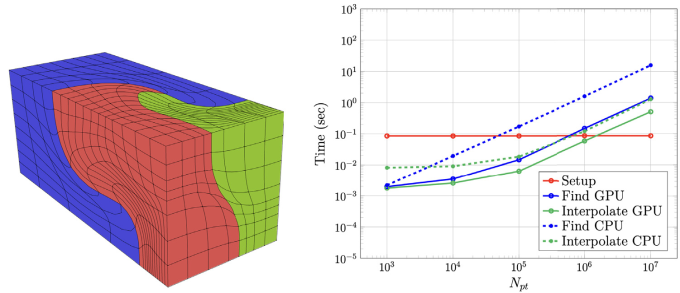
The team’s bounding approach builds on previous work on the findpts library, which was created by Lottes to evaluate points on 2D quadrilateral and 3D hexahedral meshes on computers with central processing units (CPUs). This new research extends point evaluation to surface meshes and to GPU-based programming, which is now ubiquitous in high performance computing (HPC) including for the Department of Energy’s (DOE) supercomputers. In fact, the upgraded calculations perform better on GPUs than on CPUs (Figure 2).

Figure 2: Left: A cubic mesh is distributed across three MPI ranks (denoted by colors) and refined to contain 65,536 elements. Right: The time to find and interpolate the mesh’s points is initially faster on CPUs (dashed lines) when the number of points is low. However, the team’s method quickly scales on GPUs (solid lines) as the number of points increases (x-axis). This example was run on LLNL’s Lassen supercomputer. (Click to enlarge.)

These capabilities are already integrated into the Livermore-led MFEM (Modular Finite Element Methods) software library and Argonne National Laboratory’s Nek5000 spectral elements solver. Both projects played important roles in the DOE’s Exascale Computing Project and continue to serve the computational math and HPC communities.

This powerful, scalable technique has already proven useful for various applications including Lagrangian particle tracking (such as in fluid flow simulations), high-order mesh optimization, and overlapping grids to solve PDEs in complex geometries. Mittal notes, “There’s really nothing like this approach in the research literature.” He and Kolev have expanded the technique described in this paper to generalized bounding of high-order finite element functions, demonstrating its impact on validating high-order meshes. The new work is detailed in a preprint co-authored with Tarik Dzanic, Livermore’s seventh Fernbach Postdoctoral Fellow.

— Holly Auten