Download the PDF version of this newsletter.
In This Issue:
- From the Director
- Collaborations | EQSIM: Earthquake Simulation Using the SW4 Code
- Lab Impact | zfp: Fast and Accurate Data Compression for Modern Supercomputing Applications
- Advancing the Discipline | UMap and Metall: ECP Products Under the Argo and SICM Projects
- Machine Learning & Applications | ExaLearn: Co-design Center for Exascale Machine Learning Technologies
From the Director
Contact: Jeff Hittinger
“No one can whistle a symphony. It takes an orchestra to play it.” – Halford Luccock
The U.S. Department of Energy now has two exascale-class machines—literally capable of “billions of billions” (1018) floating point operations per second—and LLNL’s El Capitan will soon make that three. However, with this scale of capability came new challenges to realize its potential in terms of the software stack, the algorithms, and the applications. In 2017, the nearly two-billion-dollar DOE Exascale Computing Project (ECP) was created to jumpstart our nation’s ability to benefit from incredible scale of computing, and LLNL—and CASC in particular—have been important performers playing their parts in the symphony that is ECP. This fiscal year, the ECP successfully concluded as an outstanding example of what the DOE national laboratories and their partners can achieve working in concert.
In this issue of the CASC Newsletter, we celebrate the success of the ECP by featuring four examples of contributions CASC made to this symphony. We start by introducing the EQSIM earthquake simulation project that relied on highly performant advanced numerical methods developed in CASC to reach record-breaking fidelity using exascale resources. This project is a great example of the power of algorithms: While the exascale hardware was only fifty times more capable than the state-of-the-art in 2017, the project demonstrated roughly three orders of magnitude speed-up. In the second offering, we discuss the zfp lossy compressed array algorithm, which offers an alternative floating point representation that can reduce both memory capacity and bandwidth usage—key concerns on modern HPC architectures.
Staying with the theme of memory, we discuss UMap, a library that enables custom memory page management, which can flexibly and scalably support the more complex memory access patterns we see in modern scientific computing while exploiting deeper memory hierarchies, e.g., node-local flash solid-state drives (SSDs). Finally, we present the ExaLearn project, an effort to enable scientific machine learning to benefit from exascale resources by building on CASC’s LBANN toolkit for parallelizing the training of convolutional neural networks.
Of course, these are just four of dozens of ECP projects in which CASC participated or led. You can find out more about LLNL’s ECP involvement at the official ECP website. My congratulations and thanks go out to all of our researchers who helped to contribute to the success of the ECP. It was a wonderful performance. Well done!
Collaborations | EQSIM: Earthquake Simulation Using the SW4 Code
Contact: Anders Petersson
Earthquake hazards and risks are a problem of national importance. The damage that could result from a large earthquake is a bigger societal problem than most people imagine. According to the U.S. Geological Survey and the Federal Emergency Management Agency, earthquakes cost the nation an estimated $14.7 billion annually in building damage and related losses. As part of the ECP, the EarthQuake SIMulation (EQSIM) application development project has created a high performance computational tool set, with the goal of removing the computational limitations as a barrier to simulation-based scientific exploration of earthquake phenomenology, hazard, and risk assessment.
At the heart of EQSIM is a wave propagation code called SW4 (Seismic Waves, fourth order) that was originally developed by CASC researchers Anders Petersson and Bjorn Sjogreen. SW4 is a summation-by-parts finite difference code for simulating seismic motions in a 3D model of Earth. It incorporates both a material model of an area (e.g., the San Francisco Bay Area) and a rupture model along a specific fault, such as the Hayward or San Andreas faults. At the start of the EQSIM project in 2017, the SW4 code could capture ground motions up to 2 Hertz in a model of the Bay Area where the shear speed exceeds 500 m/s. These calculations could, for example, be executed on 1,024 nodes of the Cori multi-core machine at LBNL and took about 24 hours to complete.
The basic challenge of high frequency seismic wave simulations is that the computational grid must be fine enough to capture the waves that are propagated through the model. In a viscoelastic material, the shortest wavelength is proportional to the slowest wave speed divided by the highest frequency. Because a fixed number of grid points are needed per wavelength, the number of grid points in the 3D model must be increased by a factor of 8 every time the frequency is doubled. In addition, doubling the frequency makes the waves oscillate twice as fast in time and therefore requires the number of timesteps to be doubled.
As a result, every time the frequency is doubled, the computational effort increases 16-fold. The goal of the EQSIM project was to increase the frequency resolution in the Bay Area model from 2 to 10 Hertz while reducing the simulation time from 24 to 5 hours. Increasing the frequency from 2 to 10 Hertz makes the simulation 625 times harder. Factoring in the additional reduction in runtime from 24 to 5 hours results in a total speedup goal of a factor of 3,000.
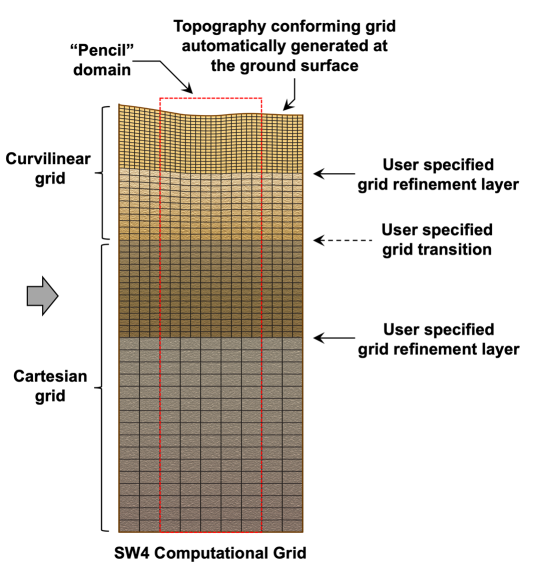
One of the most significant algorithmic improvements during the EQSIM project was to completely modify the mesh used by the SW4 code. At the beginning of the project, SW4 combined a curvilinear grid near the model surface to follow the Earth’s topography and a Cartesian grid at depth for improved efficiency. Both grids had about the same grid size, which had to be fine enough to resolve the motion through the slowest material in the model, near the surface. The saving grace of seismic wave simulations is that the material wave speeds are only very low near the top surface and are often an order of magnitude larger below the MoHo discontinuity, near the bottom of the computational domain at 30 km depth. This makes seismic wave simulations an ideal candidate for local mesh refinement.
For example, in the San Francisco Bay Area, the shear wave speed exceeds 1,000 m/s below a depth of 800 meters. If the lowest wave speed near the surface is restricted to 500 m/s, this means that the finest grid is only needed in the top 800 meters of the model and can be doubled below depth 800 meters. Further grid coarsening can be made once the wave speed exceeds 2000 m/s, and so on. While the benefits of the mesh coarsening are conceptually easy to understand, the details of its implementation are quite involved. The EQSIM project developed a carefully designed mesh coarsening algorithm that ensures time-stepping stability through energy conservation and retains overall fourth order accuracy of the solution [2][5]. An example of the resulting mesh is shown in Figure 1.
With the mesh coarsening algorithm in hand, the researchers could further improve the realism of their Bay Area simulations by more accurately representing the shear wave speed in the top 800 meters of the model. Thus, instead of restricting the shear wave speed to exceed 500 m/s, the work enabled the capture of shear wave speeds down to 140 m/s by further refining the mesh near the surface. The resulting mesh for the Bay Area model has 391 billion grid points, of which 80% are in the top 145 meters of the model.
While the algorithmic improvements of SW4 were important, the code also had to undergo significant software changes to run well on CPU-based multi-core machines, or GPU-based hardware. Early in the EQSIM project, the researchers made the decision to use the RAJA library to achieve portability across different hardware platforms. This library allows essentially the same C++ source code to be compiled to run on either CPU-based multi-core machines using OpenMP for multi-threading, or GPU-based machines using backends for Cuda, HIP, or Sycl.
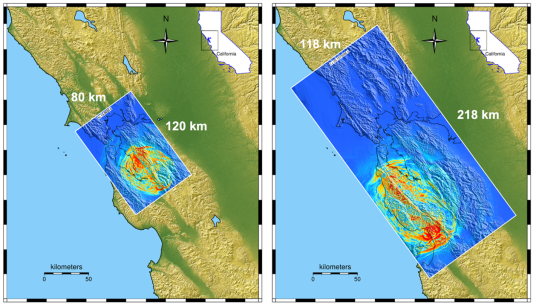
The key performance prediction (KPP) metric for the EQSIM project was defined for a scenario magnitude 7.0 earthquake on the Hayward fault in the Bay Area model. Starting at the normalized value of KPP=1 in 2017, thanks to great teamwork within EQSIM and help from the RAJA team, the EQSIM project finally reached KPP=3,500 on the Frontier system in September of 2023. Late in the project, the increased capabilities of SW4 allowed the group to consider a much larger rupture with magnitude 7.5 on the San Andreas fault. Snapshots from both the Hayward and San Andreas simulations are shown in Figure 2.
[1] D. McCallen, et al. “Regional-scale fault-to-structure earthquake simulations with the EQSIM framework: Workflow maturation and computational performance on GPU-accelerated exascale platforms,” Earthquake Spectra., 2024, doi:10.1177/87552930241246235.
[2] L. Zhang, S. Wang, and N. A. Petersson, “Elastic wave propagation in curvilinear coordinates with mesh refinement interfaces by a fourth order finite difference method,” SIAM J. Sci. Comp., 2021, 43(2):A1472–A1496.
[3] D. McCallen, et al. “EQSIM - a multidisciplinary framework for fault-to-structure earthquake simulations on exascale computers part I: computational models and workflow,” Earthquake Spectra, 2021 37(2):707–735, doi:10.1177/8755293020970982.
[4] A. Rodgers, et al. “Regional-scale three-dimensional ground motion simulations of MW 7 earthquakes on the Hayward Fault, Northern California resolving frequencies 0-10 Hz and including site response corrections,” Bull. Seismo. Soc. Amer., 2020, 110(6):2862–2881.
[5] S. Wang and N. A. Petersson, “Fourth order finite difference methods for the wave equation with mesh refinement interfaces,” SIAM J. Sci. Comput., 2019, 41(5):A3246–A3275, arXiv:1809.04310.
[6] H. Johansen, et al. “Toward Exascale Earthquake Ground Motion Simulations for Near-Fault Engineering Analysis,” Comput. Sci. Eng., 2017, 19(5):27–37.
Lab Impact | zfp: Fast and Accurate Data Compression for Modern Supercomputing Applications
Contact: Peter Lindstrom
The zfp data compression algorithm epitomizes efficiency and versatility in the realm of data storage and transmission. With its unique support for random access to data elements coupled with guarantees on either storage size or numerical accuracy, zfp offers a dynamic solution tailored to diverse applications, from scientific simulations to Big Data analytics. By balancing compression ratios and data integrity, zfp is able to achieve resource-efficient data management and numerical computations, empowering users to optimize storage space and enhance computational performance with unparalleled ease and effectiveness.
zfp was developed by a team of LLNL researchers led by CASC computer scientist Peter Lindstrom and includes ASQ computer scientists Danielle Asher and Mark C. Miller. In addition, three former Lab employees—Stephen Herbein, Matthew Larsen, and Markus Salasoo—were part of the team. zfp [1] presents a new compressed number format for floating-point and integer arrays intended to reduce in-memory and offline storage and transfer time of large data sets that arise in HPC. zfp effectively expands available CPU and GPU memory by as much as 10x; reduces offline storage by one to two orders of magnitude; and—by reducing data volumes—speeds up data movement between memory and disk, distributed compute nodes, CPU and GPU memory, and even main memory and CPU registers. Such reductions in data movement are critical to today’s HPC applications, whose performance is largely limited by data movement rather than compute power.
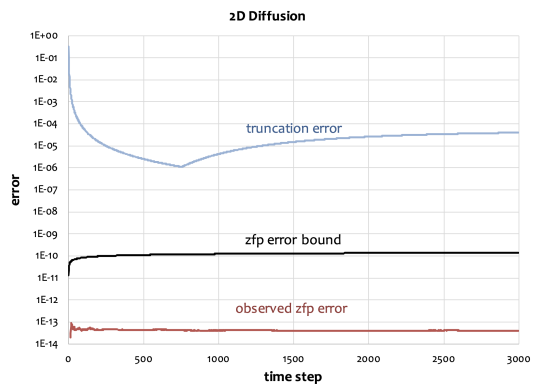
Unlike the majority of today’s lossy file compressors [2,5], quite a bit is known about the numerical errors introduced by zfp’s lossy compression modes. For instance, it is known that the zfp error distributions are essentially normal (or Gaussian), but with finite support (i.e., errors are bounded) due to the mixing of uniform roundoff errors that occur in its decorrelating transform. This normality is attractive as it allows a user to reason about the propagation of such errors; e.g., the sum of two normal random variables is also normal. Moreover, the errors can be shown to be unbiased and uncorrelated [3], which is important in many physics applications to ensure conservation of mass, energy, and momentum, and in statistics. Absolute error bounds for zfp compressed data have been established [4], which allow scientists to set an acceptable error tolerance wherein zfp reduces the data as much as possible while respecting the tolerance, as shown in Figure 3.
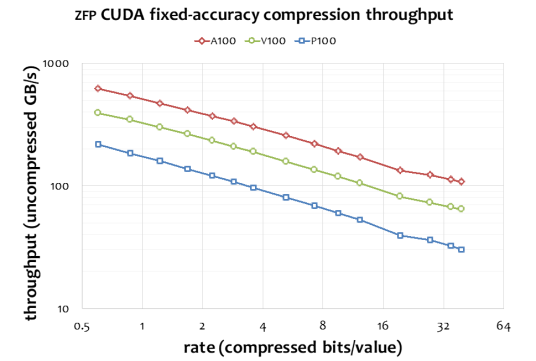
One important consideration, especially for accelerating data movement via compression, is the speed of compression and decompression. That is, to realize a net performance gain in data transfers, the total time spent on compression (by the sender), transfer of compressed data, and decompression (by the receiver) must not exceed the time needed to transfer the data uncompressed. As documented extensively through numerous publications, zfp is one of the fastest—if not the fastest—lossy numerical compressor available [5]. The zfp CUDA-based GPU implementation achieves up to 700 GB/s throughput in compression and decompression, as shown in Figure 4. This is substantially faster than the throughput of I/O, supercomputer interconnects, and PCI Express for channeling data between CPU and GPU. Several success stories of using zfp to accelerate I/O [6], communication, and CPU-GPU transfers [7] have demonstrated speedup factors of up to 40, 6, and 2.2, respectively.
zfp is recognized as one of the leading solutions for numerical data compression and has consequently seen widespread adoption in industry, academia, and national labs. With over 1.5 million measurable downloads per year (from GitHub, Anaconda, and PyPI), the following features are largely responsible for zfp’s impact and rapid adoption:
- Unique features like random access, prescribed and guaranteed memory footprint, and fine-grained access not supported by other compressors
- Effectiveness at compressing data, competing with best of breed
- Floating-point compressor speed (fastest available)
- High parallelizability by design
- Attractive error properties and error guarantees not available through other compressors
- C, C++, Python, and Fortran bindings, with other language bindings available through third parties (Rust, Julia, and WebAssembly)
zfp has been used in SW4 earthquake simulations (see EQSIM article above) and NIF HYDRA simulations, and is supported by the Livermore Equation of State (LEOS) library, to name a few applications. It also has been adopted by various Intel products, the MVAPICH MPI library, ArcGIS, and others. In 2023, it won the prestigious R&D 100 award.
[1] P. Lindstrom, “Fixed-rate compressed floating-point arrays,” IEEE Transactions on Visualization and Computer Graphics, 2014, 20(12):2674–2683, doi:10.1109/TVCG.2014.2346458.
[2] R. Ballester-Ripoll, P. Lindstrom, and R. Pajarola, “TTHRESH: tensor compression for multidimensional visual data,” IEEE Transactions on Visualization and Computer Graphics, 2020, 26(9):2891–2903, doi:10.1109/ TVCG.2019.2904063.
[3] D. Hammerling, A. Baker, A. Pinard, and P. Lindstrom, “A collaborative effort to improve lossy compression methods for climate data,” IEEE DRBSD-5, 2019, 10.1109/DRBSD-549595.2019.00008.
[4] J. Diffenderfer, A. Fox, J. Hittinger, G. Sanders, and P. Lindstrom, “Error analysis of zfp compression for floating-point data,” SIAM Journal on Scientific Computing, 2019, 41(3):A1867–A1898, doi:10.1137/18M1168832.
[5] S. Li, P. Lindstrom, and J. Clyne, “Lossy scientific data compression with SPERR,” IPDPS 2023, doi:10.1109/IPDPS54959.2023.00104.
[6] P. Lindstrom, P. Chen, and E.-J. Lee, “Reducing disk storage of full-3D seismic waveform tomography (F3DT) through lossy online compression,” Computers & Geosciences, 2016, 93:45–54, doi:10.1016/j. cageo.2016.04.009.
[7] L. Noordsij, S. van der Vlugt, M. Bamakhrama, Z. Al-Ars, and P. Lindstrom, “Parallelization of variable rate decompression through metadata,” Euromicro PDP 2020, doi:10.1109/PDP50117.2020.00045.
Advancing the Discipline | UMap and Metall: ECP Products Under the Argo and SICM Projects
Contact: Maya Gokhale
Today’s emerging exascale workloads are expected to incorporate data-intensive processing in close coordination with traditional physics simulations. These emerging scientific, data analytics, and machine learning applications need to access a wide variety of datastores in flat files and structured databases. Programmer productivity is greatly enhanced by mapping datastores into the application process’s virtual memory space to provide a unified “in-memory” interface. A team of researchers in CASC, led by Maya Gokhale and includes Roger Pearce, Keita Iwabuchi, and CASC alumnus Ivy Peng, have developed two products, called UMap and Metall, that can help address this need by optimizing applications’ interactions with large, out-of-core datastores.
UMap is part of the ECP Argo project, which is focused on augmenting and optimizing existing operating system and runtime components. By exploiting locally attached flash solid-state drives (SSDs) that can reduce the divide between storage and memory, the research team built UMap [1][2], which is a user-level file memory mapping library, to access non-memory-resident data. Peng, who has since left the Lab, was the primary developer of UMap while she was a CASC researcher. With a pluggable datastore manager, the UMap library enables development of custom memory page management strategies tuned to access patterns of highly concurrent, multi-threaded applications. UMap’s advantages include high flexibility to configure page size and queue management, scalability at large thread counts, and extensibility to future-proof the library.
The research team prioritized four design choices for UMap based on surveying realistic use cases. First, they chose to implement UMap as a user-level library so that it can maintain compatibility with the fast-moving Linux kernel without the need to track and modify for frequent kernel updates. Second, they employed the recent userfaultfd mechanism to reduce overhead and performance variance in multi-threaded applications. Third, they targeted an adaptive solution that sustains performance even at high concurrency for data-intensive applications, which often employ a large number of threads for hiding data access latency.
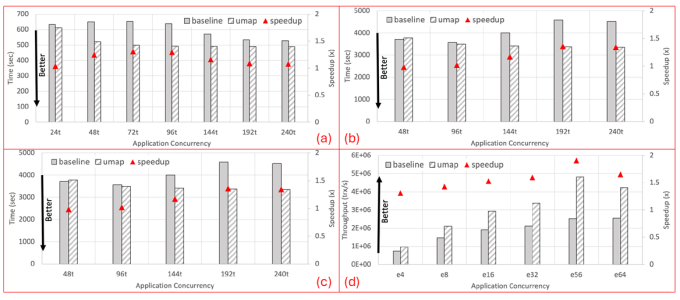
Finally, for flexible and portable tuning on different computing systems, UMap provides both API and environmental controls to enable configurable page sizes, eviction strategy, application-specific prefetching, and detailed diagnosis information to the programmer. UMap as a userspace service outperforms an optimized kernel-based mmap service across a wide range of intra-node concurrency at a level of 22–90%.
Analogous to heap management libraries for data in main memory, the research team also created Metall [3], a persistent memory allocator that stores dynamically allocated persistent objects in memory-mapped files. Metall is part of the ECP SICM project, which is focused on addressing the emerging complexity of exascale memory hierarchies. Applications that generate and analyze complex data structures rely on dynamic allocation and release. Metall enables applications to transparently allocate custom C++ data structures into various types of persistent memories. It incorporates a concise and high performance memory management algorithm inspired by Supermalloc and the rich C++ interface developed by Boost.Interprocess library.
Metall achieved performance improvements of up to a factor of 11.7 and 48.3 over Boost.Interprocess and memkind (PMEM kind), respectively, on a dynamic graph construction workload. To optimize storage of the Metall persistent heap, the research team developed the Privateer library [4], which optimizes I/O performance and storage space at the abstraction level of virtual memory and backing store management. Karim Youssef was the primary developer of Privateer; he is currently a postdoc in CASC. Privateer uses private memory-mapping with optimized writeback and content-addressable data storage and can deliver 30% storage space improvement for storing snapshots of an incrementally growing graph while delivering comparable performance to the baseline Metall.
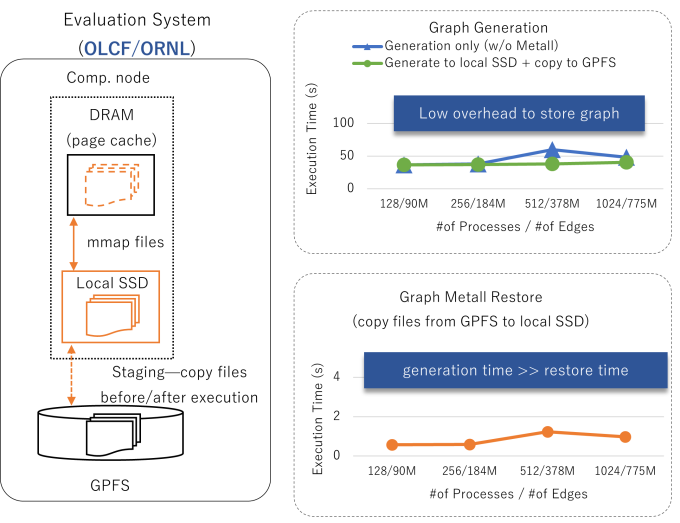
In terms of application, Metall has been integrated into MiniVite, which is a distributed graph community detection application that is part of the ECP proxy application suite. In this application, graph generation takes up to 20 times longer than the analytics and is a bottleneck in timely graph analysis. By using Metall, MiniVite can perform graph generation once, and then store and re-use use graph objects in the Metall persistent heap. Figure 6 shows the use of Metall in MiniVite on the ORNL Summit and Crusher systems. The generated graph is copied to the global file system for long term storage, and then copied to local SSD for use in a graph analytic, reducing analytic startup time by more than an order of magnitude.
[1] I. Peng, et al., “UMap: enabling application-driven optimizations for page management,” Proc. IEEE/ACM Workshop Memory Centric High Performance Computing, 2019, pp. 71–78.
[2] I. Peng, M. Gokhale, K. Youssef, K. Iwabuchi, and R. Pearce, “Enabling scalable and extensible memory-mapped datastores in userspace,” IEEE Transactions on Parallel and Distributed Systems, 2022, 33(4):866–877, doi:10.1109/TPDS.2021.3086302.
[3] K. Iwabuchi, K. Youssef, K. Velusamy, M. Gokhale, and R. Pearce, “Metall: A persistent memory allocator for data-centric analytics,” Parallel Computing, 2022, vol 111(102905), ISSN 0167-8191, doi:10.1016/j.parco.2022.102905.
[4] K. Youssef, K. Iwabuchi, W.-C. Feng, and R. Pearce, “Privateer: multi-versioned memory-mapped data stores for high-performance data science,” IEEE High Performance Extreme Computing Conference (HPEC), 2021, pp.1–7.
Machine Learning & Applications | ExaLearn: Co-design Center for Exascale Machine Learning Technologies
Contact: Brian Van Essen
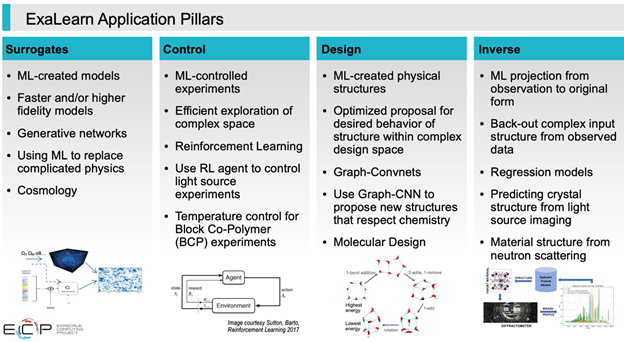
In 2018, ECP created the ExaLearn project to develop AI/ML algorithms and tools that were optimized for the emerging advanced technology and leadership-class exascale HPC systems that were coming online. It was an eight-lab effort that focused on developing scientific machine learning (SciML) with a particular thrust on four methodology pillars: surrogate, control, inverse, and design models and methods. Within each of these pillars, exemplar applications were selected as the focus of the project.
Additionally, multiple cross-cut thrusts were created, which included scalability and performance, I/O, proxy applications, and workflow. The LLNL team, led by CASC researcher Brian Van Essen, was responsible for the scalability and performance cross-cut and worked with the surrogate application pillar to develop unique capabilities and algorithms optimized for the Exascale systems.
Focusing on the interplay between achieving strong scaling on large SciML models and developing surrogates for scientific simulations, the LLNL team developed novel methods in the LBANN toolkit for parallelizing the training of convolutional neural networks along the spatial, channel, and filter dimensions. This allowed the training and inference of neural network architectures on simulation volumes that were previously inaccessible with traditional deep learning toolkits.
This is exemplified by LBANN’s application to CosmoFlow and CosmoGAN models from LBNL. CosmoFlow is a deep learning tool that allows for the determination of the initial condition (IC) parameters of a Universe based on the simulated 3D distribution of mass in the Universe using 3D convolutional neural networks, and CosmoGAN applies Generative Adversarial Networks to the problem of generating weak lensing convergence maps. The LLNL team used both low- and high-resolution simulations from Nyx to train CosmoFlow and CosmoGAN.
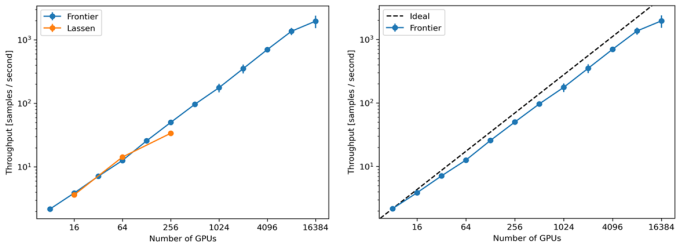
For CosmoFlow, the expectation is that a high granularity (5123, 10243, or larger) input will allow the determination of the ICs with high precision. Its end product is the ability to infer cosmological parameters such as matter density and perturbation amplitudes, spectral index, and Hubble’s constant from a simulation or a surrogate model. The LBANN team has been experimenting with adjusting the loss function to handle a variety of physical and spectral constraints. Using LBANN to move to the full 3D CosmoFlow data sets has shown that the generator network produces maps that are described by the same summary statistics as the fully simulated maps, with high statistical confidence. Using the parallelization strategies developed by the LLNL team, ExaLearn was able to demonstrate the scalable training of the CosmoFlow model on both Lassen and the Frontier system at ORNL as part of the ECP KPP-3 milestone, using up to 16,000 GPUs.
LBANN also demonstrated the ability to generate high-fidelity surrogates from a trained model with CosmoGAN in a fraction—0.01%—of the time it takes to run a Nyx simulation. They performed the demonstration run on the Lassen system at LLNL and published their findings in [1]. They also performed a demonstration run on the Frontier system at ORNL, using an updated CosmoFlow model that has been aligned with the MLPerf HPC version and updated to work with 5123 volumes.
Additionally, the LLNL team developed custom 3D convolutional compute kernels that were optimized for the unique dimensions encountered within these SciML models. The first high-level result achieved was a 58.11-factor speedup on Frontier with respect to Lassen when using 16,000 GPUs of Frontier versus 256 GPUs of Lassen. Looking at the relative performance on only Frontier shows a 39.20x speedup using 16,000 GPUs versus 256 GPUs. This led to a set of parallel efficiencies on Frontier of 0.72x for 256 GPUs and 0.44x for 16,000 GPUs.
[1] Y. Oyama, et al. “The case for strong scaling in deep learning: training large 3D CNNs with hybrid parallelism,” IEEE Transactions on Parallel and Distributed Systems, 2020, 32(7):1641–1652.
CASC Newsletter Sign-up
Was this newsletter link passed along to you? Or did you happen to find it on social media? Sign up to be notified of future newsletters.
Edited by Ming Jiang. LLNL-MI-865782