Disclaimer: This article is more than two years old. Developments in science and computing happen quickly, and more up-to-date resources on this topic may be available.
Download the PDF version of this newsletter.
In This Issue:
- From the Director
- Collaborations: Enabling Rapid COVID-19 Small Molecule Drug Design Through Scalable Deep Learning of Generative Models
- Lab Impact: High-Order Finite Elements for Thermal Radiative Transfer on Curved Meshes
- Advancing the Discipline: Fast and Accurate Data Race Detection for OpenMP Programs
- Machine Learning & Applications: NM-ROM: Marrying Machine Learning with Reduced Order Models
- Highlights
From the Director
Contact: Jeff Hittinger
“Adversity has the effect of eliciting talents, which in prosperous circumstances would have lain dormant.” – Horace
Who knew when we scrambled to transition to shelter in place that we would still be here one year later? In many ways, that seems like last week, but in others, it feels like a lifetime ago. Either way, it has been amazing to witness the resilience of CASC and our ability to shift our entire way of work, while still maintaining our productivity and the high quality research for which we are known
That is not to say that it has been easy. There is isolation without the daily comradery, the serendipitous meetings, and the lunches with friends and colleagues. Some of us have worked for the Lab for nearly a year and have never been on site. Some of us have children who have struggled with online learning and who have lost an important year in their childhood. Some of us have lost loved ones.
We look forward to returning to a more normal time and take hope in the recent advances in treatments and vaccines for COVID-19. Still, we have not stopped advancing our discipline. In this issue, we are proud to highlight several research activities that are truly pushing the boundaries of what is possible in scientific computing: in the application of new methods and capabilities to pressing problems like COVID-19 therapeutic discovery, in foundational work creating new modeling and simulation algorithms, and in advanced tool development to enable more effective use of high performance computing (HPC).
Collaborations | Enabling Rapid COVID-19 Small Molecule Drug Design Through Scalable Deep Learning of Generative Models
Contact: Sam Ade Jacobs
The Accelerating Therapeutics for Opportunities in Medicine (ATOM) consortium was established as a public-private partnership with the primary purpose of accelerating drug discovery by creating an open and sharable platform that integrates HPC, emerging biotechnologies (leveraging artificial intelligence), and shared biological data from public and industry sources. LLNL is a leading member of the ATOM consortium, and CASC staff have been part of the consortium from its inception.
The pandemic has presented opportunities to leverage the variety of skills within the consortium to address the challenges of COVID-19. Whereas significant effort has been devoted to the development of preventative vaccines for COVID-19, there is also need for the development of therapeutic options like therapeutic antibodies and small molecule antivirals. CASC’s collaborative efforts within ATOM focus on discovering and designing candidates for small molecule antivirals.
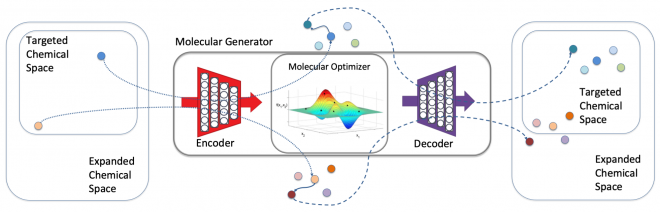
In the drug design landscape, there are an estimated 1060 compounds from which to identify as potential drug candidates. Exploring this landscape to find appropriate drugs is a herculean task and costly both in time and effort. With the increased availability of large compute resources and techniques from the machine learning (ML) community, the LLNL team’s goal has been to leverage ML techniques to optimize new molecules within a large design space based on the docking, binding, and molecular dynamics information from promising known molecules (see Figure 1).
To this end, the team designed a Wasserstein autoencoder, a generative model that is both computational efficient and of higher quality than existing state-of-the-art methods. Leveraging a LLNL open-source, HPC-centric ML toolkit (LBANN), the team trained the autoencoder on an unprecedented 1.6 billion drug compounds—nearly an order of magnitude more chemical compounds than any other work reported to date.
For drug design, the ability to train generative models at scale provides an opportunity for chemists and domain scientists to explore the chemical space with a speed and at a scale not seen before. The scalable parallel algorithm implemented in LBANN enabled rapid prototyping and training of the large-scale molecular generator within reasonable runtime: The novel WAE model was trained on 1.6 billion compounds in 23 minutes, while the previous state-of-the-art solution required a day for only 1 million compounds.
Thus, training at such an unprecedented scale—using all of the Sierra supercomputer—can benefit and extend the frontiers of discovery for drug design, accelerating the search for novel candidate drugs and reducing the time to synthesize such compounds to be tested in the laboratory.
In terms of ML at HPC scale, whereas there have been applications of ML techniques in drug design space, this work enabled by CASC researchers is the first to demonstrate such applications at a billion (drug) compound scale on a pre-exascale system. The LLNL team worked with researchers from NVIDIA on optimization of different compute kernels for performance scalability. Training the ML model at HPC scale also exposed the need for algorithmic choices to promote power optimization at extreme scale. For example, asynchronicity in ML algorithms was necessary to avoid dramatic power usage swings at the Livermore Computing leadership-class facility (see Figure 2).
This CASC effort is part of a large, multidisciplinary team that was recognized as a special-topic SC20 Gordon Bell finalist paper [1]. Authors on the Gordon Bell submission come from different disciplines, divisions, and directorates at LLNL: Sam Ade Jacobs, Brian Van Essen, and David Hysom are computer scientists in CASC; Felice Lightstone, a biochemist from the Physical and Life Sciences Directorate, currently leads LLNL COVID-19 small molecule project; Jonathan Allen is a bioinformatician in the Global Security Computing Applications Division (GS-CAD) and a project lead within ATOM; Tim Moon, Kevin McLoughlin, and Derek Jones are (bio) data scientists within GS-CAD; and Ian Karlin, John Gyllenhaal, and Py Watson are with Livermore Computing. The team also benefited from the expertise of a long list of other collaborators both within and outside LLNL.
[1] S. A. Jacobs, T. Moon, K. McLoughlin, D. Jones, D. Hysom, D. H. Ahn, J. Gyllenhaal, P. Watson, F. C. Lightstone, J. E. Allen, I. Karlin, and B. Van Essen, “Enabling Rapid COVID-19 Small Molecule Drug Design Through Scalable Deep Learning of Generative Models,” to appear as Gordon Bell Special Prize finalist in International Journal of High Performance Computing Applications (IJHPCA), 2020.
Lab Impact | High-Order Finite Elements for Thermal Radiative Transfer on Curved Meshes
Contact: Terry Haut
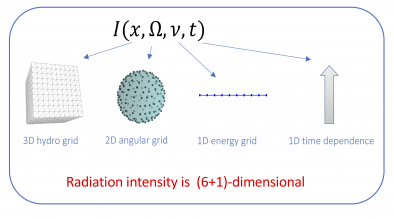
The accurate modeling of thermal radiative transfer (TRT), which describes the interaction of radiation with a background material, is a critical component of LLNL’s mission. TRT simulations are extremely challenging because of the high-dimensional nature of the models describing photon transport (see Figure 3). Given that the next-generation Arbitrary Lagrangian-Eulerian (ALE) hydrodynamics code uses high-order (HO) finite elements on HO curved meshes, an outstanding research problem has been how to robustly couple TRT and hydrodynamics on the HO curved meshes.
LLNL’s current production deterministic TRT code can only solve the TRT equations on low-order (LO, straight-edged) meshes, which necessitates mapping solutions from the native HO mesh to an LO refined mesh. This mapping procedure necessarily entails an increase in the degrees of freedom by factors of 4 in 2D and 8 in 3D (relative to solving on the native HO mesh), and it can be several orders of magnitude more for the highly distorted meshes that arise from HO Lagrangian hydrodynamics (see Figure 4).
Given TRT’s enormous memory footprint and runtime, decreasing the number of unknowns needed to represent the TRT system can have a significant impact on LLNL’s multi-physics simulations. In addition, solving the TRT equations on the hydrodynamics mesh avoids potential instability and physics degradation resulting from HO to LO mappings.
This challenging problem was the topic of a recently concluded Laboratory Directed Research and Development (LDRD) project led by CASC researcher Terry Haut and involving Vladimir Tomov (CASC), Milan Holec (CASC), Ben Yee (now at WCI/DPD), Sam Olivier (UC Berkeley), Will Pazner (CASC), Ben Southworth (now at LANL), and Pete Maginot (now at LANL).
To solve the TRT equations using HO finite elements on HO meshes, this team developed a novel, graph-based HO SN transport solver [1], which is efficient even on highly distorted HO Lagrangian hydrodynamics. They also developed several physically motivated preconditioners based on HO variants of discretized diffusion equations [2-5] and data-driven methods [6]; such preconditioners are critical in the common regime where photons are frequently absorbed and reemitted by the material.
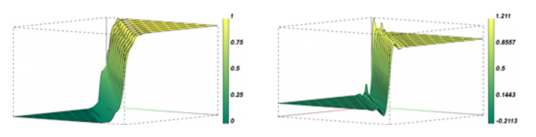
To avoid solutions with unphysical oscillations and negative values in spatially under-resolved regions, which is a common occurrence for HO methods, the team also developed a new positivity-preserving, conservative transport solver that preserves a discrete maximum principle and has negligible computational overhead [7]. Importantly, this positivity-preserving scheme does not degrade the convergence of the main HO diffusion-type preconditioner, which has been an open research question even for LO methods (see Figure 5).
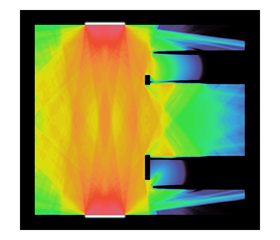
Finally, the team led by Haut developed several new nonlinear solvers and IMEX time-stepping schemes for HO TRT [8-10] and have demonstrated their efficacy on challenging inertial confinement fusion (ICF) problems, including the ICF problem based on a 2D (X-Y) model of throttled radiative flux in a half-hohlraum, which is motivated by the National Ignition Facility (NIF) Sonoma campaign (see Figure 6).
One noteworthy feature of the IMEX time-stepping schemes is the need for only a single so-called SN transport sweep for meshes with convex mesh elements, which can save significant computational time in comparison to standard methods.
This work was presented at the 2020 Predictive Science Panel (PSP) Deep Dive at LLNL to a panel of external experts. In the PSP final report, the panel recommended that LLNL develop these methods within a production code for use by the next-generation multi-physics code. Work on a next-generation TRT code for production use is currently under way, which will leverage the research developed in this LDRD to enable HO discretizations on HO meshes and coupling with LLNL’s next-generation multi-physics code.
[1] T. S. Haut, P. G. Maginot, V. Z. Tomov, B. S. Southworth, and T. A. Brunner, “An Efficient Sweep-Based Solver for the SN Equations on High-Order Meshes,” Nuclear Science and Engineering, pp. 746–759, 2019.
[2] T. S. Haut, B. S. Southworth, P. G. Maginot, and V. Z. Tomov, “DSA Preconditioning for DG Discretizations of SN Transport and High-Order Curved Meshes,” SIAM Journal of Scientific Computing (in press), 2020.
[3] B. S. Southworth, M. Holec, and T. S. Haut, “Diffusion Synthetic Acceleration for Heterogeneous Domains, Compatible with Voids,” Nuclear Science and Engineering (in press), 2020.
[4] S. S. Olivier, P. G. Maginot, and T. S. Haut, “High Order Mixed Finite Element Discretization for the Variable Eddington Factor Equations,” in International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering, 2019.
[5] S. S. Olivier, “On Fast Solvers for the Variable Eddington Factor Equations,” in International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering, 2021.
[6] R. G. McClarren and T. S. Haut, “Acceleration of Source Iteration using the Dynamic Mode Decomposition,” in International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering, 2019.
[7] B. C. Yee, T. S. Haut, M. Holec, V. Z. Tomov, and P. G. Maginot, “A Quadratic Programming Flux Correction Method for High-Order DG Discretizations of SN Transport,” Journal of Computational Physics, 2020.
[8] M. Holec, B. S. Southworth, T. S. Haut, W. Pazner, and B. C. Yee, “Multi-Group Nonlinear Diffusion Synthetic Acceleration of Thermal Radiative Transfer,” in International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering, 2021.
[9] T. S. Haut, M. Holec, B. Southworth, B. Chang, W. Pazner, B. Yee, and S. Olivier, “A New One-Sweep Implicit-Explicit Time-Stepping Scheme for Thermal Radiative Transfer,” in International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering, 2021.
[10] B. C. Yee, S. S. Olivier, B. S. Southworth, M. Holec, and T. S. Haut, “A New Scheme for Solving High-Order DG Discretizations of Thermal Radiative Transfer using the Variable Eddington Factor Method,” in International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering, 2021.
Advancing the Discipline | Fast and Accurate Data Race Detection for OpenMP Programs
Contact: Ignacio Laguna and Giorgis Georgakoudis
OpenMP is the de facto standard for on-node parallelism in HPC, targeting both multicore CPUs and accelerators such as GPUs and also serving as the backend of high-level programming models, such as RAJA and Kokkos. Although OpenMP is widely used, writing correct OpenMP programs can be difficult, as data race conditions and other concurrency bugs can be easily introduced. Debugging race conditions in OpenMP is particularly challenging because of the non-deterministic behavior of parallel programs.
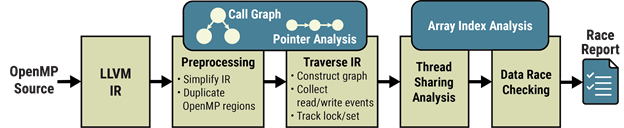
CASC researchers Ignacio Laguna and Giorgis Georgakoudis, along with academic and industry collaborators, have been pushing the envelope on developing new methods for data race detection in OpenMP. The majority of the current work on race detection focuses on dynamic tools—i.e., tools that detect a race by tracing the program’s execution. That approach, however, has several limitations: (1) It is slow because of the high overhead associated with memory tracing, and (2) detection depends on the specific thread and input configuration, so it may miss data races that do not manifest with a specific configuration. CASC researchers have developed a static approach, called OMPRacer, that overcomes the limitations of existing methods. OMPRacer does not require running the program and can detect all the races in the program, including those that dynamic methods detect and those that they miss.
OMPRacer leverages the LLVM compiler’s intermediate representation (IR) to statically analyze the parallel execution of OpenMP regions in a program. It discovers parallel OpenMP regions to build a concurrency graph that encodes concurrent logical tasks, the data they use along with their sharing attributes, and any synchronization specified using OpenMP. Based on this novel analysis of parallelism in the compiler, OMPRacer detects concurrent memory accesses that can result in data races, independently of the specific input and thread configuration at runtime (see Figure 7).
As a tool, it is easy to integrate OMPRacer in the build configuration of an application: It requires as input only the source code, without the need of tracing, and provides a comprehensive data race report as the output that pinpoints possible data races in the source code. Compared to other state-of-the-art static and dynamic data race detectors, including ARCHER, benchmarked with DataRaceBench, OMPRacer has the highest detection accuracy (91%). Table 1 shows relevant results. Comparing its execution time to ARCHER using HPC proxy applications, OMPRacer’s static approach is on average faster by avoiding application execution for tracing.
| Tools | Precision | Recall | Accuracy | Total Accuracy |
|---|---|---|---|---|
| ARCHER | 0.98–0.98 | 0.91–0.91 | 0.94–0.95 | 0.90 |
| ROMP | 0.96–0.96 | 0.91–0.91 | 0.93–0.93 | 0.85 |
| LLOV | 0.83 | 0.94 | 0.86 | 0.63 |
| OMPRacer | 0.89 | 0.93 | 0.89 | 0.91 |
The techniques behind OMPRacer as well as a comprehensive evaluation of the method were published as a technical paper at the SC20 conference [1]. OMPRacer’s ideas were initially developed in a collaboration project with researchers at Texas A&M University. Later this project led to the creation of a startup, Coderrect, which is commercializing a software tool for static data race detection.
[1] B. Swain, Y. Li, P. Liu, I. Laguna, G. Georgakoudis, and J. Huang, “OMPRacer: A Scalable and Precise Static Race Detector for OpenMP Programs,” in Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, pp. 1–14, 2020.
Machine Learning & Applications | NM-ROM: Marrying Machine Learning with Reduced Order Models
Contact: Youngsoo Choi
In the past decade, ML has excelled in using large amounts of data to produce predictive models where first principles hardly exist, such as in speech recognition, self-driving cars, protein-folding, writing short sentences with perfect grammar, and AlphaGo. However, one area where ML lacks robustness is in physical simulations. This shortcoming is partly because data-driven neural networks (NNs) fail to incorporate known first principles, such as conservation properties. The result has been that an ML-based, black-box approach to physical modeling has lacked accuracy and physical fidelity.
Recently, some ML researchers have realized the importance of incorporating first principles. The physics-informed NN (PINN) [1] is a representative example. Although the PINN has demonstrated a new way to incorporate first principles knowledge into the ML framework and provided a way of obtaining a solution without complete information about initial and boundary conditions, these networks are slower and less accurate than existing numerical methods because their solution process relies on the training of the NNs. Thus, there is a need for better ways to combine the power of ML with existing numerical methods to achieve acceleration and accuracy.
Physics-constrained reduced order models (ROM) provide an approach to fully leverage the benefits of data-driven models within existing numerical methods by reducing the size of the corresponding full order model (FOM). Among the many ROM approaches used, the Linear Subspace ROM (LS-ROM)—in which a linear subspace solution representation is used—has been successfully applied to various decision-making applications as well as to many physical simulations. Despite its successes, the LS-ROM solution representation is not able to represent certain physical simulation solutions in a compact form, such as the solution to advection-dominated problems over long time periods. These limitations call for a new way of representing the solution (e.g., a nonlinear manifold solution representation that can be achieved by ML).
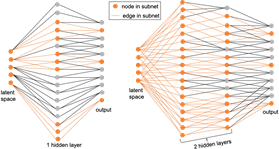
In collaborative work with researchers in LLNL’s Computational Engineering Division, CASC researcher Youngsoo Choi recently developed a nonlinear manifold ROM (NM-ROM) technique [2,3] that overcomes this gap by substituting the nonlinear manifold solution representation (which is trained with ML) into the numerically discretized governing equations. NM-ROM also exploits a special NN structure to achieve a speed-up (Figure 8). The NM-ROM introduces a new way of incorporating first principles with ML and shows how to re-use existing numerical methods in the ML-based, data-driven physical simulations.
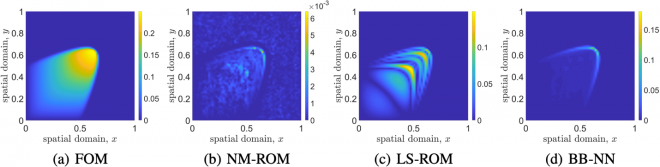
Figure 9 shows the comparison of the FOM solution and the predictions of various data-driven models for the parameterized advection-dominated 2D Burgers’ equation, with a large Reynolds number of 10,000. Figure 9(a) shows the FOM solution (a finite difference approximation) at the final time and (b–d) show absolute differences of the FOM solution and three different data-driven models at the final time. The NM-ROM outperforms both the LS-ROM and black-box neural network (BB-NN) methods in terms of accuracy (note the scale differences), presenting a promising pathway for improved modeling. In this example, the FOM solution has 3,600 degrees of freedom, while all the data-driven models use a latent space dimension of five and use the same data. The NM-ROM approach is eleven times faster than the FOM. Both LS-ROM and BB-NN are unable to capture the FOM solution accurately. Here, LS-ROM and NM-ROM follow the methods described in [2,3], while BB-NN follows the method described in [4].
The successful application of the NM-ROM on the 2D Burgers’ equation is promising because the estimates predict that the NM-ROM will achieve much greater speed-up for larger-scale problems while preserving sufficient accuracy. If these estimates hold for more complex problems, many decision-making problems that require ensembles of calculations, such as uncertainty quantification, design optimization, optimal control, and inverse problems, could be computed using NM-ROMs fairly quickly—if not in real time—which would enable breakthroughs in science and engineering applications.
[1] M. Raissi, P. Perdikaris, and G. E. Karniadakis, “Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations,” Journal of Computational Physics, 378, pp. 686–707, 2019.
[2] Y. Kim, Y. Choi, D. Widemann, and T. Zohdi, “Efficient Nonlinear Manifold Reduced Order Model,” accepted in Workshop on Machine Learning for Engineering Modeling, Simulation and Design at NeurIPS, 2020.
[3] Y. Kim, Y. Choi, D. Widemann, and T. Zohdi, “A Fast and Accurate Physics-Informed Neural Network Reduced Order Model with Shallow Masked Autoencoder,” arXiv preprint, arXiv:2009.11990, 2020.
[4] B. Kim, V. C. Azevedo, N. Thuerey, T. Kim, M. Gross, and B. Solenthaler, “Deep Fluids: A Generative Network for Parameterized Fluid Simulations,” in Computer Graphics Forum, vol. 38, no. 2, pp. 59–70, 2019.
CASC Highlights
A lot has happened since our last newsletter.
New Postdocs (Since June 2020)
- Jingyi (“Frank”) Wang (6/20)
- Tahsin Reza (7/20)
- Ryan Vogt (7/20)
- Siu Wun (“Tony”) Cheung (7/20)
- Mark Heimann (8/20)
- Trevor Steil (11/20)
- Michael Barrow (11/20)
- Haichao Miao (12/20)
- Zoe Tosi (1/21)
- Brendan Keith (2/21)
New Staff Hires (Since June 2020)
- Matthew Sottile (7/20)
- Tom Benson (7/20)
- Milan Holec (7/20)
- Yohann Dudouit (8/20)
- Michael Wyatt (8/20)
- Nai-Yuan Chiang (8/20)
- Keita Iwabuchi (9/20) – transfer from GS-CAD
- Kshitij Bhardwaj (10/20)
- Jim Gaffney (10/20) – transfer from PLS
- Braden Soper (10/20) – transfer from GS-CAD
- Quan Bui (11/20)
- Jayram Thathachar (11/20)
- Jize Zhang (1/21)
- Ben Priest (1/21)
Departures (Since July 2019)
- Abhinav Bhatele (8/19)
- Milo Dorr (10/19) – retired/returned as subcontractor
- Qunwei Li (10/19)
- Dean Williams (10/19) – retired
- Avary Kolasinski (1/20)
- Ben Yee (1/20) – transfer to WCI
- Bryce Campbell (3/20)
- Naoya Maruyama (4/20)
- Sasha Ames (8/20) – transfer to GS-CAD
- Todd Gamblin (8/20) – transfer to LC
- Scott Lloyd (8/20)
- Louis Howell (8/20) – retired
- Nathan Hanford (10/20) – transfer to LC
- Sookyung Kim (1/21)
- Andrew Barker (4/21)
CASC Newsletter Sign-up
Was this newsletter link passed along to you? Or did you happen to find it on social media? Sign up to be notified of future newsletters.
Edited by Ming Jiang. LLNL-WEB-821743