Disclaimer: This article is more than two years old. Developments in science and computing happen quickly, and more up-to-date resources on this topic may be available.
Lightweight and stiff, lattices are important structures in the design of many strong materials—particularly those bearing an external load, such as a scaffold for tissue regeneration or a medical implant. Computer simulations have long been the milieu for exploring lattice shapes and identifying desirable properties, but solving just one design optimization (DO) problem in two or three dimensions comes with huge computational costs.
A patent obtained by Center for Applied Scientific Computing (CASC) researchers Youngsoo Choi and Sean McBane provides a fast, flexible, and accurate way to optimize lattice design. The patent describes a computational and numerical solution for assembling joint and strut components in any lattice topology. This component-wise reduced order modeling (CWROM) method enables high-fidelity lattice DO hundreds of times faster than with traditional finite element methods.
Approximation with Accuracy
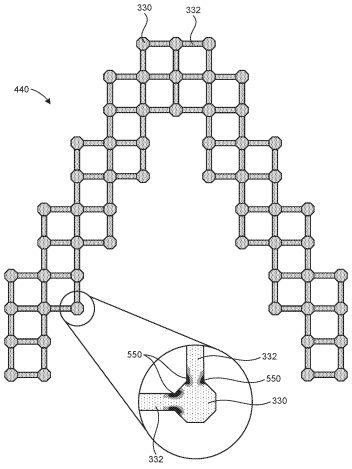
The features that make lattices attractive in materials design and manufacturing—joints and struts, and the interfaces between them, arranged in repeated patterns—also make them incredibly complex to simulate under stress conditions. Approximation schemes are necessary to lessen the computational burden and narrow the viable design space, but these can fall short of providing meaningful DO.
For example, homogenization methods apply infinite boundary conditions to reduce computational complexity at the expense of accuracy on the lattice’s surface. Beam/truss methods achieve computational speed-ups with one-dimensional modeling between joints, but the accuracy suffers at joints where a lattice often fails.
Building off a CWROM method developed at the Massachusetts Institute of Technology, McBane (who graduated from the University of Texas at Austin and now works in industry) extended the concept during his LLNL summer internship, integrating ROM into DO routines that solve lattice problems under load conditions. The resulting patented technology overcomes the deficiencies of homogenization and beam/truss methods—and at a lower computational cost.
“CWROM doesn’t require infinite boundary conditions,” explains Choi, who mentored McBane. “All components are modeled in two or three dimensions, making the model more accurate and with the same resolution as corresponding high-fidelity methods.” The method is flexible enough to allow users to define a structure’s dimensions, pattern, components, and other characteristics.
Beyond Lattices
Choi points out that CWROM can be used beyond lattices to materials with repeated patterns and where a need exists to reduce weight while maintaining structural integrity and strength, such as a helmet or airplane wing. “Simulations can capture pieces of a physical phenomenon expensively,” he notes. “Our technology is a physics-informed machine learning method that preserves important physical properties, such as conservation of mass. CWROM solves these simulation challenges nicely.”
In addition to the patent, the team has published two papers in Computer Methods in Applied Mechanics and Engineering: Component-wise reduced order model lattice-type structure design and Stress-constrained topology optimization of lattice-like structures using component-wise reduced order models. Working with additional CASC staff and a Rice University collaborator, they plan to apply CWROM to nonlinear problems, combining a neural network with ROM techniques to continue improve accuracy and data compressibility. Choi states, “CWROM offers exciting capabilities to physicists, chemists, and materials scientists. With application to any type of physical problem, we see many opportunities for this technology.”
—Holly Auten