The gollnlp project addresses mathematical and computational challenges arising in the optimization of today’s electrical power grids. Our goal is to develop the methodology and software needed to solve such mathematical optimization problems rapidly and robustly in real-time operations of the U.S. transmission power grids. Central to our approach is the use of affordable, cost-realistic high performance computing (HPC) hardware and the generally available HPC software stack. This project responds to the Grid Optimization (GO) Competition launched by the U.S. Department of Energy’s Advanced Research Projects Agency – Energy (ARPA-E) to develop computational and software management solutions for a reliable, resilient, and secure American electricity grid.

Team

Core activities are performed at LLNL, while personnel at the University of California, Merced, develop technologies for contingency screening.

  • Cosmin G. Petra (principal investigator, petra1@llnl.gov) is a computational mathematician/computer scientist at LLNL’s Center for Applied Scientific Computing. His work focuses on algorithms and HPC solvers for the mathematical optimization of extreme-scale engineering systems with emphasis on complex energy systems.
  • Ignacio Aravena (aravenasolis1@llnl.gov) is an operations research engineer in LLNL’s Computational Engineering Division. His work focuses on developing optimization models (mixed-integer, nonlinear, stochastic) and scalable/parallel algorithms to improve power systems’ resilience.
  • Omar DeGouchy, PhD student, University of California, Merced.
  • Juraj Kardos, PhD student, Università della Svizzera italiana, Lugano (while at LLNL).

The team receives valuable support and guidance from professors Roummel Marcia (University of California, Merced), Olaf Schenk (Università della Svizzera italiana, Lugano), and Joey Huchette (Rice University).

Highlights

  • Capability to optimize in real-time transmission power grids with as much as 70,000 buses without running into algorithmical or computational limitations.
  • Uses mathematically sound nonlinear programming algorithms and state-of-the-art scientific computing.
  • The optimization engine for SC-ACOPF uses an asynchronous parallel computing model to enable high parallel efficiency and robust computations.

The Security-Constrained AC Optimal Power Flow Problem

Power flow optimization problems are one of the central challenges in electrical power grid operations and planning, upon which depends the cost efficient and safe provision of electricity to industrial, commercial, and residential consumers. The nation's drive toward clean energy generation and decentralized energy resources—as well as the drastic changes in demand due to the recent progress in energy storage technologies and electrical vehicles—challenge the operations paradigm of today’s electrical power grid designed around large, centralized generation plants. To address these shifts in the U.S. power grid, the Department of Energy’s Advanced Research Projects Agency – Energy (ARPA-E) launched the GO Competition to develop computational and software management solutions for a reliable, resilient, and secure American electricity grid.

ARPA-E GO Competition - Challenge 1 focuses on solving the cornerstone problem of short-term power grid operations planning: the security-constrained AC (alternate current) optimal power flow (SC-ACOPF), over realistic power grids with nationwide geographic coverage and subjected to tens of thousands of adverse grid equipment failures. These problems are characterized by their large size, nonlinearity, non-smoothness, non-convexity, and, for certain real-world grids, ill-conditioned nature. These characteristics make SC-ACOPF problems extremely challenging both mathematically and computationally. ARPA-E provides a large collection of SC-ACOPF instances and concrete performance metrics (e.g., measuring dollar-cost efficiency and robustness of the competitors’ solutions). Teams participating in the competition are required to submit their software for execution and evaluation. These two steps are performed by an independent third party—namely, Pacific Northwest National Laboratory.

The SC-ACOPF problem can be roughly stated as follows: find the power generators’ output for all generators and voltages at all grid nodes, such that

  • total operation cost is minimized;
  • demand for power is satisfied;
  • circuit equations (physics) are not violated;
  • voltage magnitude limits of buses and thermal limits of lines are respected under normal operations; and
  • voltage magnitude limits of buses and thermal limits of lines are satisfied under any possible contingency.

If written explicitly for a real-world power grid, this optimization problem would have hundreds of millions of variables and constraints. Regardless, the SC-ACOPF problem needs to be solved on a regular basis and in real time by power grid operators in order to ensure they meet security and reliability standards. The mathematical and computational complexity of the SC-ACOPF problem with the features required by today’s grid and the future grid makes it impossible for system operators to optimize over the entire decision space. In fact, the complexity of such problems even challenges the current state-of-the-art in computational optimization.

More information on the SC-ACOPF problem can be found on the competition website.

Technical Approach

Our approach involves multiple features developed for the gollnlp project, among them:

  • Decomposition of SC-ACOPF as ‘master’ subproblem (normal operation) and ‘recourse’ subproblems (contingencies)
  • Interior-point methods for nonlinear (non-convex) problems for both solving the master and evaluating the recourse subproblems
  • Advanced primal-dual warm restart across subproblems
  • Non-smoothness of recourse subproblems handled with active-set+crashing approach
  • Distributed-memory asynchronous parallelism (i.e., without a locking master process) increases load balancing and uses computational resources more efficiently
  • Low-level error/fault detection and handling for computational robustness and resilience

Results

GO Competition Challenge 1

gollnlp team ranked first on all four divisions of the GO Competition Challenge 1. ARPA-E Leaderboard can be found here. ARPA-E performed a detailed comparative analysis for the results of the gollnlp team and, in a kudos page dedicated to the LLNL team, they concluded that LLNL achieved "a very strong first place in Challenge 1" as "the team accounted for over half of the best scenario scores: 816 first places out of a possible 1408 or 58%!". Furthermore, it is noted that "even when not getting the best objective value, the LLNL team was almost always very close".

This third party comparative analysis confirmed our additional internal analysis of gollnlp Challenge 1 results. We estimated (the upper bound of) gollnlp’s optimality gap to be less than 0.2% for the great majority of the problems (95% out of a subset of 1,360 problems the team had access to). For the rest, the estimation is generally under 2%, with only four problems being between 2% and 11%. For a typical operational cost of $800,000, an 0.2% optimality gap reflects that the solution provided by gollnlp can only be improved by at most $1,600, if at all.

Ongoing Investigations

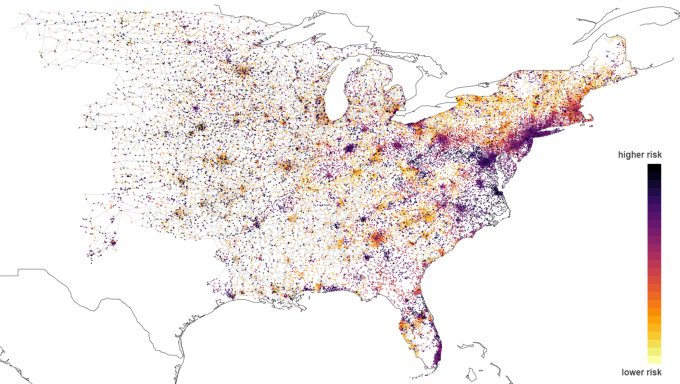
Recently, we have started to research larger scale networks using our approach. We have been able to perform SC-ACOPF analysis over grids that are more than twice the size of the problems in Challenge 1, such as the 70,000-bus synthetic system presented in Figure 1.

Figure 1. Heatmap of the risk of equipment overload for a 70,000-bus synthetic system, representative of the eastern United States, under 20,000 contingencies. gollnlp's advanced warm start and asynchronous parallelism allow it to perform extensive contingency evaluations within hard time limits (45 minutes for offline computations; 10 minutes for real-time computations)—detecting the critical contingencies leading to these overload risks and devising preventative measures to ameliorate these risks, while minimizing the operation cost.

Accessing gollnlp and SC-ACOPF test cases

Synthetic SC-ACOPF instances used in the ARPA-E GO Competition - Challenge 1 have been made available online and are maintained by the competition organization team at the Datasets section of the official competition website. These, as well as new instances, can all be tested using the ARPA-E Benchmark Code, available here.

The numerical optimization, grid modeling, and HPC approaches are detailed in a journal paper by Petra and Aravena, which can be found here. The gollnlp source code can be found on GitHub here.

Acknowledgment

This work has been funded by the Advanced Research Projects Agency – Energy (ARPA-E) and by the Advanced Scientific Computing Research Program within the Office of Science of the U.S. Department of Energy.