Known as the fourth state of matter, plasma is present in a range of physical phenomena including Earth’s magnetosphere, lightning, the northern lights, and every star in the universe. From space propulsion techniques to photolithography, humans harness plasma in numerous ways. The substance is composed of charged particles—positively charged ions and negatively charged electrons—which makes it electrically conductive, susceptible to electromagnetic forces, and inherently multiscale. A crucial part of LLNL’s high-energy-density science research involves understanding macroscopic plasma behavior under various conditions. However, because small scales and large scales in plasmas are fundamentally linked, elucidating and controlling bulk macroscopic properties often require understanding small-scale physics.
Predicting plasma behavior is as tough as describing it. Plasma temperatures can reach millions of degrees, densities and magnetization can vary widely, and a “zoo” of oscillating, unstable waves can cause properties to change rapidly while converting energy from one form to another. Furthermore, plasma dynamics cover a vast range of spatiotemporal scales that span many orders of magnitude, and tracking plasma evolution requires kinetic theory, which, in addition to bulk properties, encapsulates the complex microphysics of particle–particle and particle–wave interactions.
These phenomena are difficult to analyze theoretically and measure experimentally, so computer simulation is an essential tool in plasma physics research. Computational scientist Genia Vogman states, “Through math, physics, and numerical algorithms, we create virtual plasmas that can help us answer longstanding questions about nature and the universe, as well as provide the crucial insights needed to harness fusion energy. Kinetic simulations today are where fluid simulations were in the 1980s—nascent with vast potential for impact.”
Vogman leads a team working on the Vlasov Continuum Kinetics (VCK) code, which solves a system of partial differential equations (PDEs) in plasma kinetic theory. (VCK’s name refers to the Vlasov–Poisson and Vlasov–Maxwell PDEs that describe charged particle interactions in plasmas.) Vogman began developing the code as a PhD student at UC Berkeley, then brought it to LLNL when she became a Lawrence Fellow in 2016. She notes, “The code was inspired by a need for computationally efficient, mathematically robust, high accuracy kinetic simulations of plasma dynamics.”
Higher Order, Higher Accuracy
While plasma physics research traditionally leans on kinetic solvers that use particle-in-cell methods, VCK is different in that it solves the governing system of equations directly and ensures mathematical convergence of the discrete solution to the exact solution. Specifically, VCK uses a discretization method that converges at fourth-order accuracy, such that with each doubling of resolution, error decreases by a factor of sixteen. This method leads to higher accuracy for the associated computational cost and provides a crucial check on whether simulations produce correct results. Additionally, by enabling simulation of kinetic physics in both Cartesian and cylindrical coordinate geometries, as well as by solving the conservation-law form of the governing PDEs, VCK supports detailed investigations of phase space dynamics while ensuring important physical quantities are conserved.
These features result in high-fidelity simulations that capture the nuances and complexities of plasma physics. “We’re leveraging recent advances in how hyperbolic PDEs are solved, including advances in supercomputing capabilities, accurate high-order discretization methods, and techniques with built-in conservation properties,” Vogman explains. “VCK is at the forefront of what we can model, the accuracy to which we can model it, and the insights we can gain about so-called ‘anomalous’ physics in plasma experiments.”
Plasma Behavior in Action
Researchers at the Lab benefit from VCK’s unique insights in a range of applications, such as in expanding predictive capabilities for pulsed-power inertial confinement fusion experiments. “With VCK, researchers are probing the fundamental properties of plasmas in which magnetic pressure far exceeds thermal pressure. Such conditions exist at the edge of all magnetically confined plasmas relevant to fusion energy and space physics applications,” Vogman says. “These types of predictions help research teams optimize their experimental designs, identify the most relevant physics, and further our scientific understanding.”
In particular, the VCK team works closely with pulsed-power researchers in LLNL’s Strategic Deterrence Directorate, where the code provides crucial insights into unexplained plasma behavior and informs the magnetohydrodynamic simulations essential to the Lab’s mission. Collaborative feedback helps refine VCK’s features and performance. Vogman points out, “This partnership illustrates how new physics insights and code development go hand in hand.”
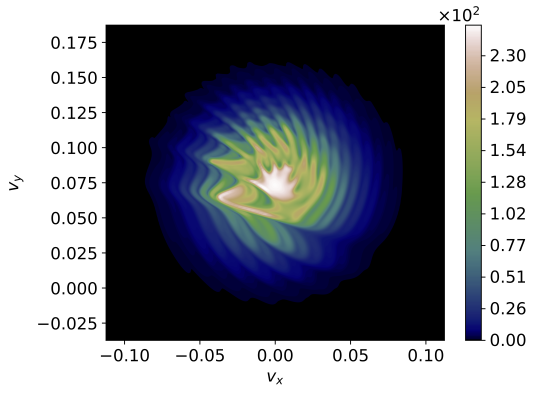
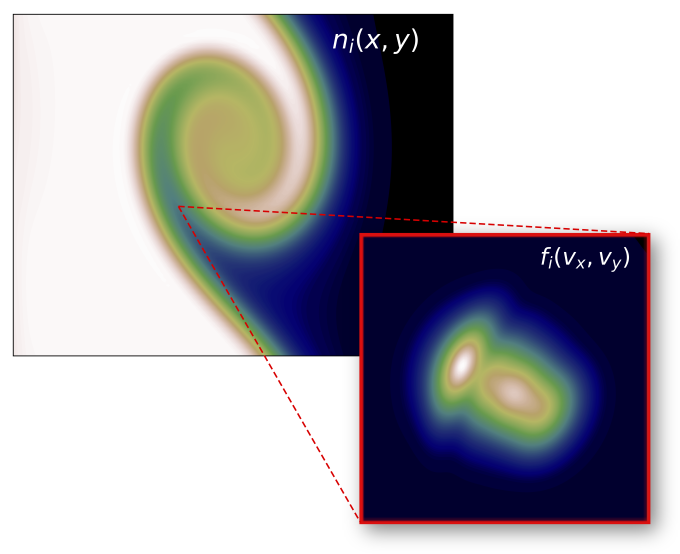
VCK is also used to study instabilities that transport plasma or convert energy from one form to another, such as the Kelvin–Helmholtz (KH) instability and those featuring microturbulence, wherein electron and ion velocity distribution functions can be far from thermodynamic equilibrium and therefore exhibit unique non-fluid behavior. For instance, Figure 1 shows a snapshot of the velocity-space ion distribution function from a VCK simulation of a magnetized plasma undergoing a lower-hybrid drift instability. In Figure 2, ion number density evolution exhibits an eddy feature that is characteristic of KH instabilities. However, because gyromotion scales and gradient scales are comparable (i.e., microphysics strongly affects macrophysics), eddy features are smeared and the local ion velocity distribution function is anisotropic.
As LLNL’s research needs and computing systems evolve, so too does VCK. The code scales to thousands of cores thanks to its parallel data infrastructure, and the team is incorporating algorithms that will allow VCK to run efficiently on GPU-based architectures such as the Lassen supercomputer and future systems like El Capitan. The VCK team’s results and advancements have appeared in numerous publications including two Physics of Plasmas papers selected as Editor’s Picks (see links in sidebar). The work has also been recognized through invited talks at the International Conference on Numerical Simulation of Plasmas and the American Physical Society Division of Plasma Physics conference.