High-Order Mapped Multiblock Framework

For a resolved solution, high-order schemes require fewer degrees of freedom (DOF) than a low-order method for an equivalent level of error. In addition, aligning the mesh with dominant flow directions reduces the resolution demands even further. Finite volume formulations are natural for systems of conservation laws, and the flux-divergence form makes extension to block-structured adaptive mesh refinement (AMR) easy. In addition, many simulation codes based on low-order discretizations are bandwidth limited – the throughput is limited by data transfer speeds such that the full computing capacity of the processor is underutilized. As explored in the Extreme Resilient Discretizations (ExReDi) project, high-order methods have better arithmetic intensity, the ratio of flops per byte transferred. Thus, high-order mapped finite volume methods have many attractive properties for conservation laws where the number of DOF need to be minimized, because of the geometric growth of DOF with dimension and/or the need to minimize data movement in modern computer architectures.

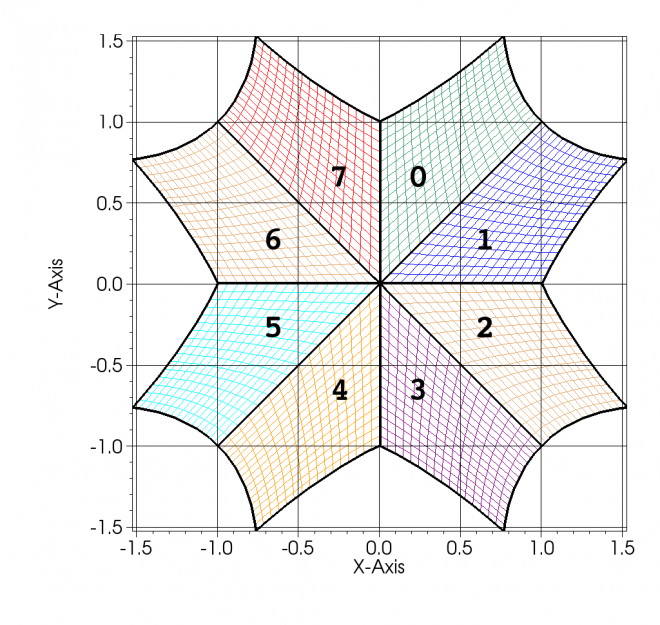
Of course, above second order, care must be taken to distinguish between point values, face-averaged values, cell-averaged values, etc. In addition, averages of products are approximated by the product of averages only up to second order, so high-order convolution and deconvolution transformations are required in addition to high-order interpolations to construct high-order fluxes. We have developed a high-order mapped finite volume formalism that addresses these issues and ensures the preservation of free-streaming, a property important for stability in mapped-grid codes. To handle complex geometries, such as the single null tokamak geometry, we have extended this formalism to multiblock grids where conformity between grids is required at the block boundaries, but each boundary has its own mapping, such that the mappings appear to be discontinuous across these interfaces. The mapping for each block extends beyond the block boundary, and a least-squares approach is used to obtain sufficiently high-order interpolations to fill ghost cells at the interfaces between blocks. In this way, the mapping on a block remains smooth.

The core capabilities for fourth-order transformations, mappings, and multiblock grids are implemented in the Chombo block-structured AMR framework.

An example mapped, multiblock grid with eight-block connectivity at a point. Note that, while the meshes are conformal at the block boundaries, the mappings are not necessarily differentiable across the block boundaries.