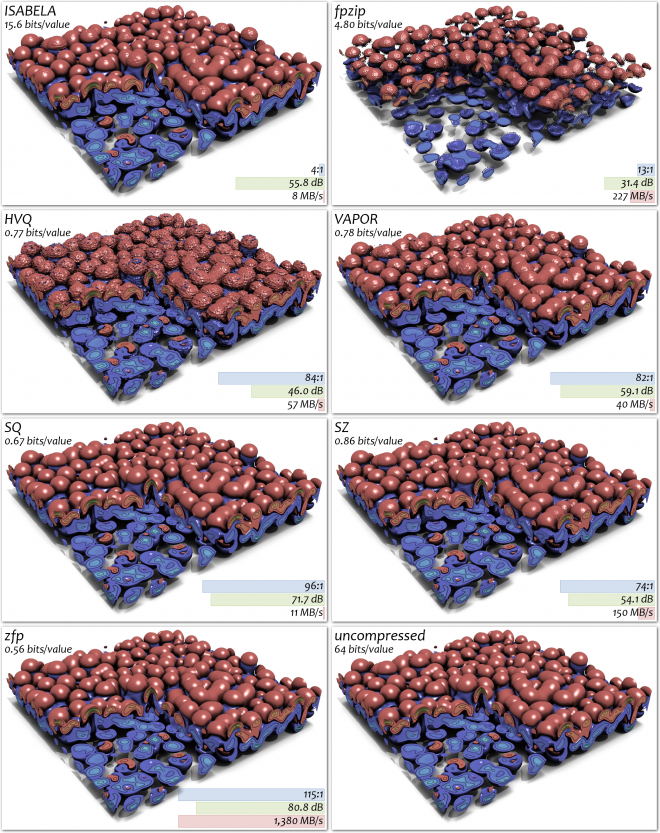
Rate-Distortion Comparisons

zfp is a very fast compressor and decompressor for floating-point data that achieves up to 2 gigabytes/second throughput. zfp also has excellent rate-distortion performance, or quality per bit of compressed storage. The images below compare the speed and quality of several published compression schemes. In addition to the compressed size in bits per value, the colored bars and numbers represent the compression ratio (uncompressed to compressed size; higher is better), peak signal to noise ratio (PSNR) in decibels (higher is better), and compression/decompression throughput in uncompressed megabytes per second (higher is better).

The original data is represented in double-precision floating point, i.e. using 64 bits/value. Notice the lack of artifacts in the zfp compressed data set, in spite of zfp using fewer bits per value than the other compressors, while also compressing and decompressing the data between 6 and 170 times faster.

The images below show using color coding the maximum (in magnitude) signed error computed along the z (vertical) direction for the data set above. This max reduction collapses the 3D volume to a 2D image. Thanks in part to zfp's fixed-accuracy mode that enforces an absolute error tolerance, it achieves low maximum errors as well.

The plot below shows rate-distortion curves for the 3D data set. Every PSNR increase of 20 dB corresponds to an additional decimal digit of accuracy. Thus zfp's 268 dB improvement over ISABELA represents an increase in accuracy (or reduction in RMS error) of more than 10 trillion times. Comparisons are also made with conversion from double to single (float) precision; truncation (zeroing) of least significant mantissa bits; and uniform scalar quantization.

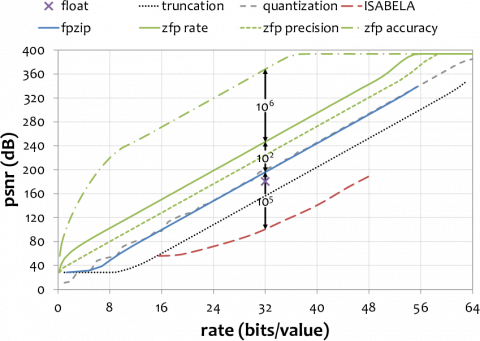
Rate-distortion plot comparing zfp with other compressors

The three green curves correspond to different modes of using zfp. In fixed-rate mode, the 3D array is partitioned into blocks of 4x4x4 values, and each block is compressed to a fixed number of bits, which enables random access at block granularity. In fixed-precision mode, the number of uncompressed bits per value is fixed, resulting in bounded relative error. In fixed-accuracy mode, each reconstructed value is guaranteed to fall within a user-specified absolute error tolerance, which usually results in the smallest RMS error and therefore highest peak signal to noise ratio for the same rate.

References