Many analysis tasks require computing spatial derivatives or other derived fields, e.g., to estimate vorticity in a turbulence simulation, or to perform topological Morse segmentation from gradients. When lossy compression is used to store the original field, such derived field computations may amplify any compression-induced errors, resulting in visual artifacts or numerical inaccuracies that were not readily apparent in the original field. Spatial derivatives are analogous to edge enhancement in image processing, and tend to reveal artifacts in lossily compressed fields.
The images below visualize the divergence of a velocity field (i.e., the sum of three partial derivatives) estimated using central differencing. The divergence field itself is not compressed; the visible artifacts are due to using lossy compression to represent the original velocity field. In spite of zfp using the least storage among all methods, its divergence field exhibits no artifacts and is visually identical to the uncompressed field.
Higher-order derivatives tend to be even more sensitive to compression-induced errors. Below are comparisons of the Laplacian fxx + fyy + fzz (sum of second partial derivatives) of an analytical function f : [-1, 1]3 → R, given by
f(x, y, z) = c (x4 + y4 + z4) - x y z - log(1 + x2 + y2 + z2)
where c = 104 / 75. Consequently, the Laplacian is given by
fxx + fyy + fzz = 2 [6 c r2 - (3 + r2) / (1 + r2)2]
where r2 = x2 + y2 + z2. The function f was chosen so that the contours of its Laplacian are concentric spheres.
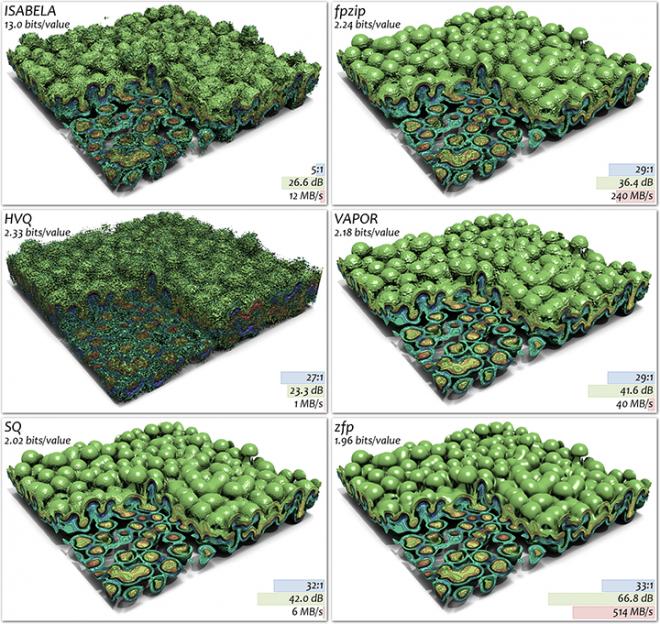
As in the case of the divergence computation above, the Laplacian is estimated using second-order central differences from the reconstructed field f that has undergone lossy compression. The bottom row below shows the zero level sets for f and its Laplacian, the latter which is a sphere of radius r = 1/2. The dark bands are highlight lines that emphasize the quality of the surface normal, which here depends on the third partial derivatives of f. As is evident, zfp provides the highest quality in the Laplacian of all compressors while using the least amount of storage. Indeed, using less than 6 bits/value, zfp achieves higher quality than 32-bit IEEE single precision floating point.
Derivatives estimated using finite differences are subject to two types of error: truncation error, which has to do with the finite support of derivative stencils (i.e., truncation of the local Taylor expansion), and roundoff error, which is due to finite precision. When estimating derivatives on a uniform grid, the truncation error decreases with finer grid spacing. The roundoff error, on the other hand, increases with finer grid spacing. This is because differences between nearby grid samples become smaller in relation to the function values themselves, and cannot be resolved well using finite precision arithmetic. For a given precision and fine enough grid, consecutive values become identical, falsely suggesting that most derivatives are zero.
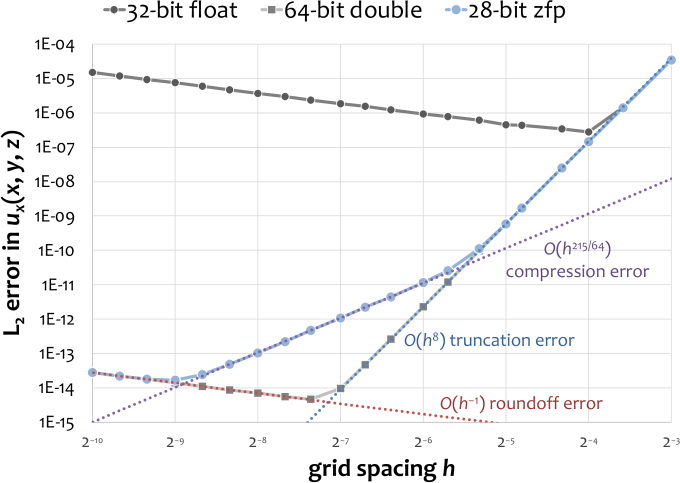
The plot above shows the L2 error in partial derivatives estimated using eighth-order central differences (this unusually high order is used here to illustrate all sources of error in the same plot). The 3D function being differentiated is sinusoidal and has analytic derivatives. The kinks in the IEEE floating-point curves are points where truncation and roundoff errors are balanced. Where this occurs depends on the numerical precision available.
In addition to truncation and roundoff error, the zfp representation incurs additional compression error, which is a form of roundoff error resulting from discarding least significant bits of the zfp fixed-rate representation to make it fit into a user-specified bit budget--here 28 bits/value. Like with truncation and roundoff error, whose convergence rates with respect to h are known, we have established the convergence rate of the zfp compression error, which depends both on h and on the dimensionality of the domain.
Paradoxically, derivatives computed from zfp's representation are often more accurate than the same derivatives computed from IEEE floating point, even when zfp uses fewer bits of storage. The zfp error curve decreases monotonically with finer grid spacing (smaller h), and eventually matches the IEEE double-precision curve. The reason for this is that zfp is far less sensitive to roundoff error. As the function is sampled more and more finely, it also locally behaves more “smoothly” and spatially correlated, which makes it easier to compress. zfp exploits that when nearby samples share many leading bits, these redundant bits need not all be stored. This frees up space for storing additional bits of precision instead, which improve accuracy and reduce roundoff error. zfp uses 62 mantissa bits internally compared to 24 respectively 53 for IEEE single and double precision, and can therefore produce more accurate derivatives (and function values) than double precision. Because zfp's decompressor returns IEEE double-precision values from which the derivatives are estimated, it is limited by the accuracy afforded by double precision. However, more accurate derivatives could in principle be computed directly from zfp’s compressed representation, i.e., without incurring the roundoff errors associated with converting from zfp to IEEE double precision.
Below we provide additional examples of zfp's ability to reduce roundoff errors in spatial derivative estimates. We use two highly nonlinear test functions whose gradient norm and Laplacian by design are closely related to the functions themselves. The first, radially symmetric function is given by
u(x, y) = (x2 + y2)3/2 / 9
on the domain [-1, 1]2. We evaluate this test function in double precision on a 4096 × 4096 Cartesian grid and then store those function values in one of several reduced-precision number representations. This conversion introduces roundoff error. We then decompress/convert the function values back to double precision and compute and plot 2nd-order finite-difference estimates of
(9 u)1/3 = (3 |∇u|)1/2 = ∆u = (x2 + y2)1/2
whose isocontours are concentric, evenly spaced circles. We compare zfp with IEEE half-, single-, and double-precision floating point and with Blaz, which like zfp is a fixed-rate compressed representation (though Blaz supports only a single rate of 5.625 bits/value).
By design, all three rows should appear the same in the absence of roundoff errors, however contours are distorted and smeared for some number formats as those roundoff errors are magnified by the differential operator. Evidently, single precision yields sufficient accuracy for first derivatives (gradients), but double precision is required for second derivatives (Laplacians); half precision is inadequate for both. Similarly, Blaz does not provide sufficient accuracy for these numerically sensitive computations. At less than one fifth the storage, 12-bit zfp, however, is qualitatively identical to full 64-bit floating point.
Our second test function is exponential:
u(x, y) = exp(4 x + 3 y)
We plot the logarithm of
u = |∇u| / 5 = ∆u / 25
whose isocontours are parallel, evenly spaced lines.
As before, only 12-bit zfp and 64-bit IEEE floating point give consistently acceptable results.