Scientists at LLNL have developed an open source, non-intrusive, and general purpose parallel-in-time code, XBraid. For source code, please see our project hosting on GitHub.

A few important points about XBraid are as follows.

• The algorithm enables a scalable parallel-in-time approach by applying multigrid to the time dimension.
• It is designed to be nonintrusive. That is, users apply their existing sequential time-stepping code according to our interface, and then XBraid does the rest. Users have spent years, sometimes decades, developing the right time-stepping scheme for their problem. XBraid allows users to keep their schemes, but enjoy parallelism in the time dimension.
• XBraid solves exactly the same problem that the existing sequential time-stepping scheme does.
• XBraid is flexible, allowing for a variety of time stepping, relaxation, and temporal and spatial coarsening options.
• The full approximation scheme multigrid approach is used to accommodate nonlinear problems.
• XBraid written in MPI/C with C++ and Fortran 90 interfaces.
• XBraid is released under LGPL 2.1.

Traditional sequential time-marching algorithms are a critical part of most computer simulations of a time-dependent problem, but these algorithms are currently facing a sequential bottleneck. This bottleneck is driven by the broad trend that future performance gains will come from greater concurrency, not faster clock speeds. Previously, ever-increasing clock speeds decreased the compute time for each time step, thus allowing more time steps to be calculated without increasing the overall compute time.

Now that clock speeds are stagnant, further refinements in time (i.e., increases in the number of time steps) will simply increase the simulation’s overall compute time. Many of these refinements in time will be required to maintain balance between spatial and temporal accuracies. Additionally, some simulations are already fully resolved in space, and it is unclear how such simulations will take advantage of the coming increases in concurrency.

LLNL researchers have advanced an alternative solution—solving for all of the time steps simultaneously, with the help of a new multilevel algorithm and the massively parallel processing capabilities of current and future high performance computers. This approach has already shown an ability to dramatically decrease the solution time for some simulations by tenfold or more.

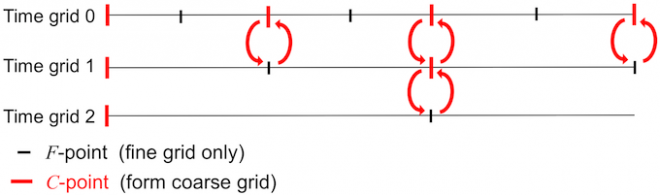
The resulting parallel-in-time method is a scalable multigrid reduction in time (MGRIT) approach. MGRIT constructs coarse time grids by coarsening every few time steps on a given level and uses each coarse time scale solution to improve the next finer-scale solution. This is depicted in the below diagram, where every other time point is chosen to form the next time grid. This yields an alternating pattern of fine (F) points and coarse (C) points. The arrows indicate how the grids communicate. The coarser time grid corrects the finer time grid solution at C-points.

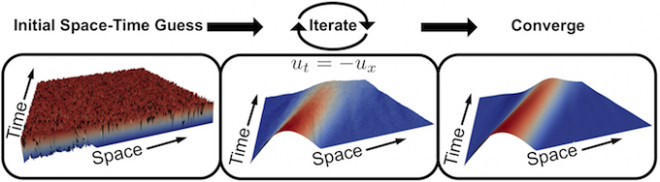
Overall, the method yields an iterative scheme that simultaneously updates in parallel a solution guess over the entire space–time domain. For illustration, the header image shows a simple one-dimensional advection equation, in which a random initial guess is iterated upon until convergence. Here, a sine wave is propagated across the domain.

Team

This pioneering effort at creating the XBraid code began in 2013 during a summer internship by Stephanie Friedhoff at LLNL, under the mentoring of Rob Falgout, Tzanio Kolev, and Jacob Schroder, and her advisor, Scott MacLachlan. The algorithmic work on MGRIT began a few years earlier.

Our team includes scientists at LLNL and throughout academia. For an up-to-date list, see this page.