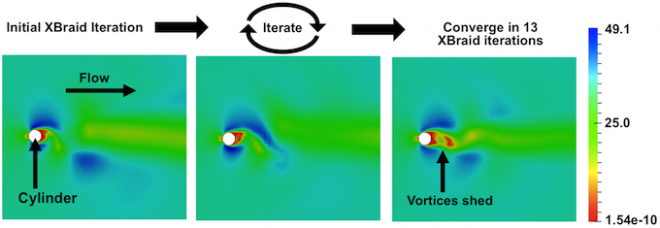
In this application, we consider applying XBraid to unsteady vortex shedding as modeled by the compressible Navier-Stokes equations over a 2D cylinder.

  • We easily coupled XBraid to the Strand2D fluids code. This involved adding only 130 lines to Strand2D, which is an existing code base of 13,500 lines. We also had to write a short XBraid wrapper for the Strand2D code.
  • Backward Euler is the time stepper.
  • 3rd order finite differencing on Strand grids is used in space. The spatial domain is defined by a graded Strand grid with a cylinder in the center, as shown next.
Graded Strand Grid
  • We use a Sandy Bridge Linux cluster with 16 cores per node and a fast Infiniband interconnect.
  • The final time is 2.56s, which is enough to capture the vortex shedding frequency.

XBraid solves for the solution quickly, offering a speedup of 7.5x in our tests. The graphic below depicts the magnitude of the velocity at the final time step as XBraid iterates over the entire space-time domain. XBraid converges in only 13 iterations to the solution at the 5,120th time step.

Vortex shedding image for unsteady compressible Navier-Stokes problem

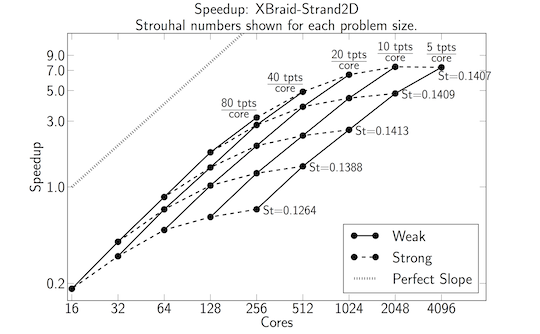
Next, a detailed strong-weak scaling study is carried out in the below plot.

  • Different numbers of fine time points per core are tried: 80, 40, 20, 10 and 5 time points (tpts) per core.
  • Dotted lines indicate a strong scaling study and represent a fixed problem size. Here the time step size and number of time steps is fixed. Only, the number of fine time points per core changes.
  • Solid lines indicate a weak scaling study. Here, the time step size is refined as the core count increases. The number of fine time points per core is fixed, as is the final time of 2.56s.
  • The Strouhal number (St) is shown next to each problem size and indicates the vortex shedding frequency. The Strouhal numbers only begin to show convergence by the final problem size. This indicates that we are not over-resolving the problem.

Regarding the performance, we can say

  • The best speedup is 7.5x and this would grow if more processors were available.
  • At smaller core counts, serial time stepping is faster. The crossover point is at 80 cores,
    where the 40 and 80 time points per core options begin to offer a speedup.
Strong-weak scaling study for XBraid applied to the vortex shedding problem.

Some algorithmic specifics are as follows (see the user's manual for more discussion of these options).

  • The temporal coarsening factor is 5 on all levels.
  • F-cycles with FCF relaxation are needed for good XBraid convergence on this problem.
  • The halting tolerance corresponds to a relative residual criteria of 10-5. With this criteria, the vortex shedding frequency (Strouhal number) agrees to within 5 decimal places between the sequential and time-parallel runs. This accuracy is sufficient.

Future work for this project will focus on the following.

  • Moving to 3D simulations.
  • Leveraging the periodic part of the solution to improve performance.
  • Optimizing the nonlinear solves on the coarse time grids