Computing applications and technology are undergoing rapid changes, and data motion is currently the limiting factor in many scientific calculations. Although modern computers possess large numbers of processors, those processors must often wait idly for data to arrive from main memory or across networks. Traditional computer memory requires continuous power to preserve data, which limits the amount of memory available per processor.
In addition, memory and network bandwidth—the rate at which data can be moved between memory and processors or between compute nodes—is not increasing as fast as the number of processing units. The net effect is that the amount of memory per core and the bandwidth per core are both decreasing on modern computers.
Researchers in Computing’s Center for Applied Scientific Computing (CASC), which applies high performance computing (HPC) and advanced computational methods to problems critical to national security, are keenly aware of the challenges posed by these constraints on data motion and storage. In the shift to accelerator-based computing using general-purpose graphics processing units (GPUs), optimal performance is only achieved by minimizing data motion between the main memory and the GPU memory. Although GPU memory is generally too small to leave data on the GPU for the duration of a computation, more efficient data representations lead to smaller memory footprints, reducing or eliminating this performance bottleneck.
“Our project is trying to speed up scientific simulations by developing new data representations and algorithms that more efficiently preserve the information encoded in the data,” says Jeff Hittinger, CASC director and Variable Precision Computing project lead.
“This project addresses one of the main issues facing the HPC community. Livermore uses scientific computing to address challenging issues across its various mission spaces, and the ability to more efficiently manage floating-point data can impact many programs, whether the primary use case is scientific simulation or data analysis,” says Hittinger.
Numerical simulations generally require the use of real numbers, that is, the infinite set of all rational numbers (integers and fractions) and irrational numbers (those that cannot be represented by a fraction, e.g., √2, e, and π). To represent all real numbers exactly would require an infinite number of bits. Instead, real numbers are approximated using a floating-point representation that maps them to a finite number of digits—e.g., π is represented as 3.14159 x 100 using six digits and an exponent.
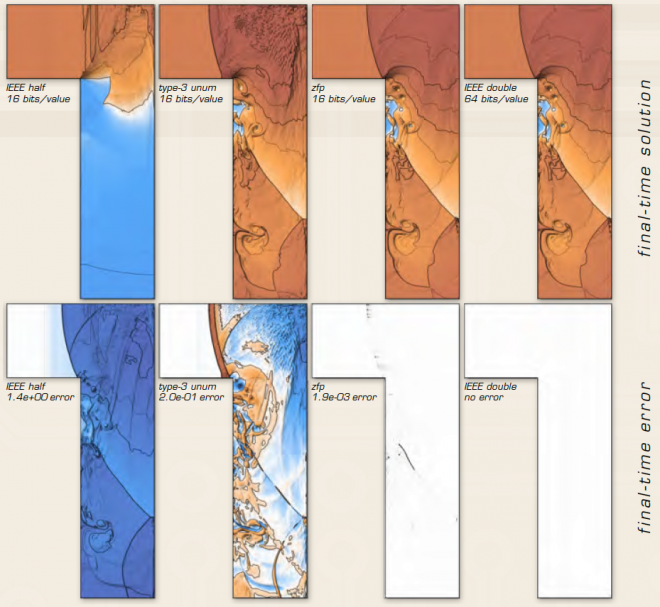
The finite nature of floating-point numbers means that only a finite number of the real numbers can be represented exactly. Single-precision (32 bits) and double-precision (64 bits) data representations are the standard (IEEE 754 Standard) floating-point implementations used in hardware. Although double-precision representation is frequently used because it reduces the effect of roundoff errors associated with floating-point arithmetic, many of the 64 bits often do not contain meaningful information—these bits represent various approximation errors—and so waste precious memory and bandwidth.
With funding from Livermore’s Laboratory Directed Research and Development program, the VPC team, including Peter Lindstrom and Dan Quinlan, is investigating new ways to reduce data size by preserving only those bits that represent useful information from a calculation.
The project’s goals are to develop: (1) representations and algorithms that reduce the amount of data with controllable precision; (2) the mathematical analysis needed to bound the errors inherent in data representations and algorithms to rigorously justify these techniques; and (3) tools to help programmers transform code to make use of these representations and to better understand the effects of finite precision on their calculations.
“We are investigating how different representations and compression algorithms can reduce the cost of data input and output and reduce the memory footprint and data transfers within a scientific simulation,” says Hittinger. In one approach, data is stored in a locally compressed data type, converted to a standard IEEE representation to apply arithmetic operations, and converted back to the compressed data type.
The VPC team is working on simulations based on partial differential equations for calculations where high precision (beyond other approximation errors) is unnecessary, a major use case for scientific computation that is easily solved using compressed data types.
“We are also developing alternative techniques for particle data, which are more difficult to compress because the data lack coherence from one particle to the next. Our compressed data types and work on low-precision algorithms also may improve the efficiency of distributed computing on sensor networks where storage and power constraints are more severe,” says Hittinger.
There is skepticism in the simulation community regarding more aggressive management of data using “lossy” compression algorithms. “For this reason, we have developed mathematical analyses to justify our approach and have developed tools to reduce the barriers to using our data-compression method,” says Hittinger.
The VPC team has also been educating people on why “lossy” is nothing new. Finite precision floating-point data representation is itself lossy; it rounds to the nearest representable number, thereby truncating bits. “The compression algorithm used in our compressed data type is more sophisticated than this and demonstrates lower resulting roundoff errors,” explains Hittinger.
In the scientific community, there is already increased interest in mixed precision—using standard IEEE types of double-, single-, and half-precision in combination to reduce memory usage in specific calculations. However, these techniques are static and can at best only provide data reductions by factors of no more than two (or four, although half-precision is by itself insufficient for numerical simulation).
“These approaches complement our work, but our goal is to develop algorithms that allow dynamic adjustment of the number of bits per value as necessary for the application,” says Hittinger.
While there is other ongoing research using data-compression techniques based on global orthogonal projections and specific data-representation changes, Hittinger says that his team’s approach is superior to those techniques because it does not need to compress or decompress entire data arrays at once, which is a burden on memory and cache.
“Our optimized floating-point data-compression algorithm, ZFP, is among the best in speed, compression rate, and accuracy. To our knowledge, we are the only group investigating compressed data types as substitutes for standard IEEE formats,” says Hittinger.