Serpentine Wave Propagation

The Serpentine project develops advanced finite difference methods for solving hyperbolic wave propagation problems, allowing for complex geometries, realistic boundary and interface conditions, as well as arbitrary heterogeneous material properties. This work is motivated by DOE applications such as estimating ground motion due to seismic events, non-destructive testing, underground facilities detection, geophysical exploration, and geothermal energy applications. In all these applications, the underlying differential equations are hyperbolic systems of second order differential form.

To overcome the limitations of traditional finite difference methods, our approach is based on solving the governing equations in second order differential formulation, using difference operators that satisfy the summation by parts (SBP) principle. Keeping the governing equations in second order formulation avoids complications due to compatibility conditions and extra boundary conditions, which must be addressed when rewriting the governing equations in first order formulation.

The SBP property of our finite difference operators guarantees stability of the scheme in an energy norm. The stability holds for heterogeneous material models on Cartesian and curvilinear grids, and allows free surface boundary conditions to be imposed on the boundary of complex domains.

In Figure 1, we show a simulation of wave propagation in a 2D elastic material, due to a point force on the free surface. When the free surface is flat, this is known as Lamb's problem. Note the bump on the left side of the free surface, which generates a secondary set of waves in the solution.

Figure 1. Magnitude of the displacement due to a point force on the free surface. The solution is shown at times t=2.6 (top) and t=7.8 (bottom). Note how the small bump on the left side of the free surface acts as a scatterer, creating a new family of P, — **Figure 1.** Magnitude of the displacement due to a point force on the free surface. The solution is shown at times t=2.6 (top) and t=7.8 (bottom). Note how the small bump on the left side of the free surface acts as a scatterer, creating a new family of P, S, von Schmidt and Rayleigh waves.

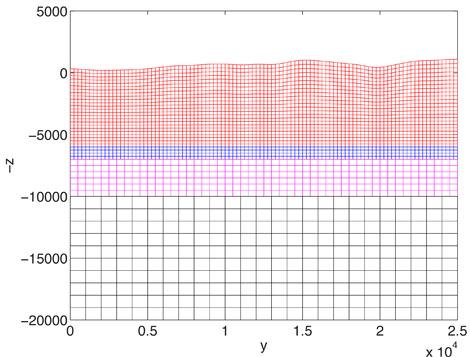
We have generalized our SBP technique to provide stable coupling conditions across mesh refinement boundaries, allowing for hanging nodes along the mesh refinement interface. This allows us to follow the velocity structure of the material model, and gradually coarsen out the computational mesh at depth. A cross-section of a typical computational grid is shown in Figure 2.

Figure 2. A composite grid with two mesh refinement interfaces and topography. In this case there are three Cartesian components and one curvilinear grid following a non-planar topography. — **Figure 2.** A composite grid with two mesh refinement interfaces and topography. In this case, there are three Cartesian components and one curvilinear grid following a non-planar topography. Visco-elastic behavior can be important when modeling the dissipative nature of realistic materials, especially for higher frequencies. We have generalized the SBP technique to the visco-elastic wave equation, where the material satisfies the rheology of standard linear solid elements coupled in parallel.

More information about SBP operators can be found on the theory page. Our publications page contains many technical papers on the stability and accuracy of our methods. Many of our methods have been implemented in the parallel open source code SW4, see our software page, where we also distribute our legacy code WPP.