Background
Linear wave propagation has traditionally been studied using the staggered-grid finite difference time domain (FDTD) method. In this approach, the second order wave equations are written as a larger first order hyperbolic system by introducing extra dependent variables. The first order system is then discretized on one Cartesian grid that covers the entire computational domain. This technique has been very popular due to its simplicity and ease of implementation, but is limited to box-shaped geometries and can only handle flat boundaries. An additional issue is that the FDTD method sometimes goes unstable when the material properties vary too rapidly on the grid.
Using a constant grid size throughout the computational domain leads to suboptimal performance when the wave speed varies across the domain, because the wave length of the solution is proportional to the wave speed of the material. The grid size is therefore dictated by the smallest wave speed in the domain. On the other hand, the time step is determined by a Courant-Freidrich-Levy condition for stability of the time-stepping, which states that the time step is limited by the grid size divided by the largest wave speed. Hence, a fixed grid size can lead to significant spatial and temporal oversampling when the material properties vary across the computational domain.
Basic finite difference methods
There are many ways of using the Finite Difference (FD) method to discretize the same partial differential equation (PDE) to the same formal order of accuracy. However, only some FD schemes work well in practice. The biggest issue is stability. We say that a FD discretization is stable when it produces an accurate solution, where the error tends to zero as the mesh size tends to zero. The rate at which the error tends to zero is known as the order of accuracy. Unfortunately, some FD discretizations are unstable when applied to time-dependent problems. This means that small perturbations, often caused by round-off errors in the finite-precision arithmetic, get amplified as the numerical solution is evolved in time. Through the power of spurious exponential growth, such perturbations can grow in time to eventually dominate the numerical solution, and cause overflows in numerical simulations.
A von Neumann analysis can be used to study the stability of a FD method with periodic boundary conditions and constant material properties. For a periodic problem with heterogeneous material properties, where the PDE satisfies an energy estimate, the energy method provides a way to ensure stability of some FD discretizations. Such FD stencils satisfy additional relations that allow a discrete energy estimate to be derived. When physical boundaries are introduced, the boundary condition must also be discretized. For complicated boundary conditions, such as the free surface boundary conditions for the elastic wave equation, it is often difficult to find a discretization of the boundary conditions that makes the overall scheme stable.
Summation by parts operators
Summation by parts (SBP) operators are a particular kind of FD stencils that generalize the energy method to bounded domains. The basic idea is to construct special FD operators that mimic the integration by parts rules, which allow an energy estimate to be derived for some PDEs in bounded domains. These FD stencils are different from the traditional FD method in that skewed (non-centered) FD stencils are used at a number of grid points near the boundary. The weights in these stencils are generally different from one point to the next point, near the boundary. For a second order accurate SBP method, the weights are only modified at the boundary itself. For higher order SBP schemes, specialized FD stencils are generally used at the first Nb grid points near the boundary. The number Nb grows with the order of accuracy. In the interior of the domain, the SBP stencil reverts to the standard FD stencil from the periodic problem.
The conditions for satisfying the SBP property for a specified order of accuracy translate into an algebraic system of equations. A computer algebra system (such as Maple or Mathematica) is often required to find a closed form solution of this system, that is the weights in the FD formulas at each grid point near the boundary. When the material properties vary in space, these formulas also prescribe how the material properties should be averaged at each grid point. Fortunately, this complicated system of algebraic equations only needs to be solved one time for each order of accuracy. Once the weights have been established, they can be coded into a numerical wave equation solver, such as SW4 or WPP.
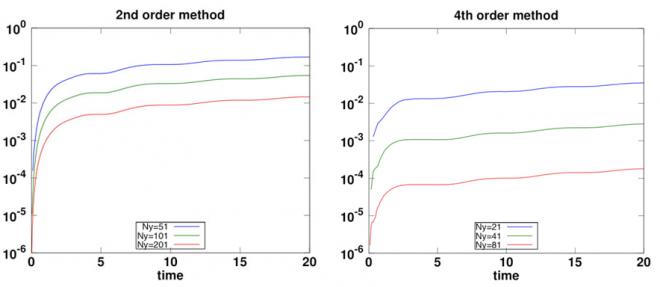
For more complicated systems of PDEs, such as the elastic wave equation with heterogeneous material properties, which has both second derivatives and cross-derivatives, additional considerations must be made when deriving the SBP stencils. A considerable amount of research on SBP stencils for first derivatives is available in the literature, and those operators can be combined for approximating the cross-terms. We have derived new SBP operators for the second derivatives that are compatible with the SBP stencils for the first derivatives, such that energy stability can be guaranteed for the overall discretization. The basic 2nd order accurate SBP method is currently implemented in the seismic wave propagation code WPP [see our software page]. Recent work shows that the 4th order SBP method is more efficient than a 2nd order method, in particular when the ratio between the P and S material velocities is high, see Figure 4. It is theoretically possible to extend our SBP technique to derive up to 8th order accurate methods, but more research is need to evaluate the efficiency of very high-order SBP methods.