Browse this site's news, projects, and people highlights via any of the topics in the dropdown list or below each content description.
Select a Topic:
PROJECTS
ASC Proxy Apps
Proxy apps serve as specific targets for testing and simulation without the time, effort, and expertise that porting or changing most production codes would require.
SAMRAI
The SAMRAI library is the code base in CASC for exploring application, numerical, parallel computing, and software issues associated with structured adaptive mesh refinement.
Legacy
VPC
Researchers develop innovative data representations and algorithms to provide faster, more efficient ways to preserve information encoded in data.
PEOPLE
Alyson Fox
Alyson Fox is a math geek. She has three degrees in the subject—including a Ph.D. in Applied Mathematics from the University of Colorado at Boulder—and her passion for solving complex challenges…
Will Pazner
LLNL has named Will Pazner as the third Sidney Fernbach Postdoctoral Fellow in the Computing Sciences.
NEWS
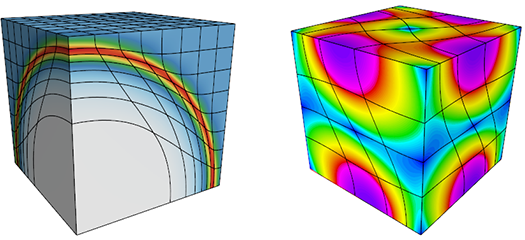
SIGGRAPH recognizes LLNL scientist and collaborators with Best Paper Award
Developed by LLNL, Colorado, and Purdue researchers, a new approach eases the implementation of curved geometries into computing simulations.
Matrix unloaded: GPU-boosted solvers for diffusion physics
Developed by LLNL and Portland State University researchers, innovative matrix-free solvers offer performance gains for complex multiphysics simulations.
Symposium paper formally verifies whether linear systems will converge
A new method defines a formal specification for convergence, which can be used to derive a set of machine-checkable conditions to guarantee a convergent solution to a differential equation.