The increasing size of scientific datasets presents challenges for fully exploring the data and evaluating an analysis approach. If the spatio-temporal variation in scientific data is not considered in the analysis, incorrect or incomplete conclusions could be drawn. In the IDEALS project, statistical and machine learning techniques are combined to give scientists and data analysts the same level of confidence in the analysis of large-scale data as they have in the analysis of small datasets, resulting in improved scientific and policy decisions.
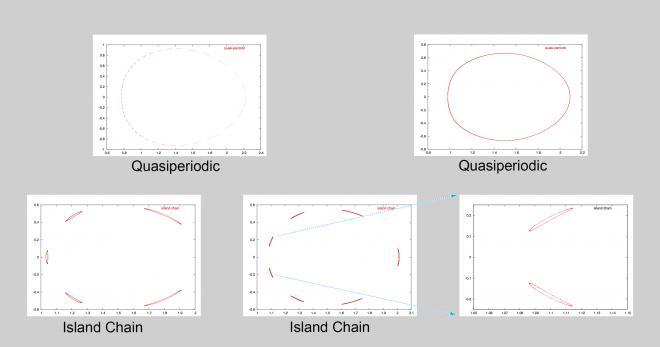
For example, if subtle differences among orbits in a Poincaré plot (Figure 1) were overlooked when planning an analysis approach to automatically assign an orbit type based on the shape traced out by a sequence of points, incorrect conclusions would have been drawn from the data. This problem worsens as the size of the data increases.
Intelligent Sub-Sampling
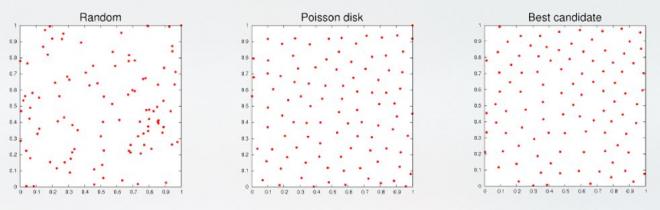
A simple and practical way to explore a large dataset is to start with a small sample. For 100 samples in a two-dimensional domain, random sampling over- or under-samples the region. Poisson disk sampling spreads the samples more evenly, but new samples are difficult to add. The best-candidate method gives good coverage and can be modified to meet our needs.
One-Pass Sampling Algorithm
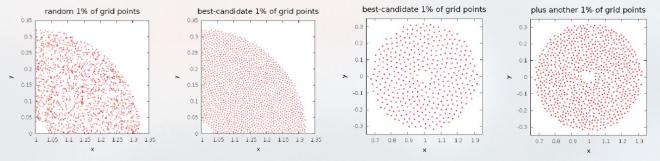
We modified the best-candidate algorithm to select a smaller subset of points, from an existing set, using a single pass through the data. If the initial set of samples is insufficient for analysis, the user can incrementally add new samples while maintaining the spread among selected samples.
Finding Interesting Regions in the Data
Having selected a subset of the grid points, we can use machine learning and statistical techniques to find “interesting” regions in the data. The single-pass variants of these algorithms can quickly indicate which regions of a large data set should be explored further. For example, we can use locally-weighted kernel regression and the values of the variable of interest at the 2% subset samples to predict the values at the remaining 98% of the data. A high error in prediction occurs where there is a lot of variation in the data, indicating an interesting region.
Learn More
The IDEALS project is funded by the Department of Energy (DOE) Advanced Scientific Computing Research (ASCR) program (Dr. Lucille Nowell, program manager). For more information, contact Chandrika Kamath.
Center for Applied Scientific Computing newsletter, vol. 1
Publications
For papers and presentations related to IDEALS, see StarSapphire Publications.