The Enabling Technologies for High-Order Simulations (ETHOS) project performs research of fundamental mathematical technologies for next-generation high-order simulations algorithms. The current focus is on advancing the theoretical understanding and practical utility of unstructured meshes with arbitrarily high-order curvilinear elements by researching key challenges associated with high-order mesh quality optimization and simulation-driven adaptivity.
With support from the Applied Mathematics research program in the Department of Energy (DOE) Office of Science, the ETHOS team performs fundamental research that is broadly applicable to many high-order simulation approaches, including high-order finite elements and tightly coupled arbitrary Lagrangian-Eulerian (ALE) simulations of interest to the DOE. Our research builds on the Target-Matrix Optimization Paradigm (TMOP) and nonlinear variational minimization to develop new node-movement strategies for high-order mesh quality optimization and adaptation in both purely geometric settings, as well as in the context of a given physical simulation.
Project summary
High-order meshes are difficult to control
- High-order simulations rely on high-order meshes, and bad mesh quality leads to small time steps and applications failures.
- In addition to good geometric quality, applications require high-order meshes to adapt to dynamic simulation features.
Our solution: Develop theory that rigorously defines high-order mesh quality
- We have extended the Target Matrix Optimization Paradigm (TMOP) by Knupp to high-order meshes, defining pointwise quality based on sub-zonal information, and optimizing the mesh node positions with respect to an aggregated quality measure. The TMOP variational minimization technique is based on optimizing an objective function that depends on a quality metric measuring the difference between the current and target geometric parameters of the mesh.
- We have extended the TMOP-based variational formulation for the GPU-based exascale architectures.
- We are currently exploring (nonlinear) solvers for the global optimization problem, meshing for automated workflows, automatic-differentiation and error-driven mesh adaptation, hrp-adaptivity, and more. Please reach out if you are interested in collaborating.
Impact: Mesh optimization is relevant to a wide range of applications. Some innovations under the ETHOS project include:
- Target construction: Methods for systematic generation of geometric target parameter values (size, aspect-ratio, skew, and orientation) that vary over mesh elements or sample points. Permits flexible and precise control over essential geometric quality features of mesh, tailored to any specific application.
- Mesh quality metrics: New polyconvex mesh quality metrics that allow control of one or more geometric parameters (size, aspect-ratio, skew, and/or orientation). Asymptotically balanced compound metrics that automatically balance mesh quality in terms of shape and size. Worst case quality improvement metrics to simultaneously untangle the mesh and decrease worst element quality.
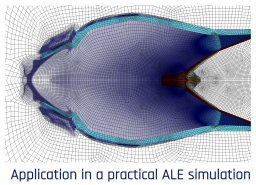
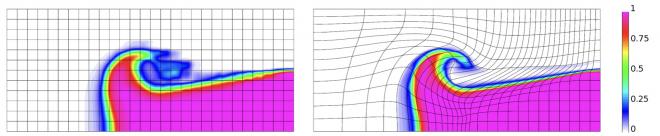
- Simulation-driven r-adaptivity: Simulation-based adaptivity to optimize meshes during runtime using the solution of the PDE. This approach has already demonstrated significant impact in improving solution accuracy and computational efficiency for ALE hydrodynamics.
- hr-adaptivity: TMOP-based energy estimators to augment r-adaptivity with anisotropic mesh refinement. hr-adaptivity is crucial when only r-adaptivity cannot meet the desired shape and size adaptivity goals.
- Surface fitting: Penalty-based formulation to align a subset of the mesh nodes to surfaces prescribed as the level-set of a discrete function. This approach is used to take a given mesh and morph it to obtain a body-fitted high-order mesh.
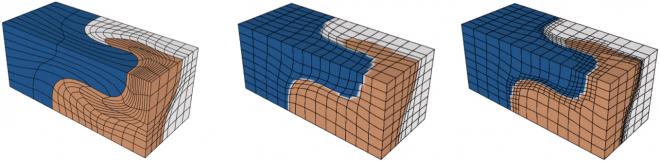
- rp-adaptivity: Surface fitting augmented with p-adaptivity such that high-order elements are only used near curvilinear surfaces and low-order elements are used elsewhere. rp-adaptivity allows us to obtain mixed-order meshes with same geometrical accuracy as a uniform-order mesh but at a much lower computational cost.
- Adaptive node limiting: Penalty-based formulation to optimize the geometric quality of the mesh while minimizing the change associated with a discrete function defined on the original mesh. This functionality was inspired by multi-material applications where it is crucial to preserve material mass for each zone while optimizing the mesh quality.
- GPU-oriented mesh optimization: Tensor factorization and matrix-free approach for TMOP-based algorithms results in orders of 20x speed-up for high-order mesh optimization in ALE hydrodynamics.
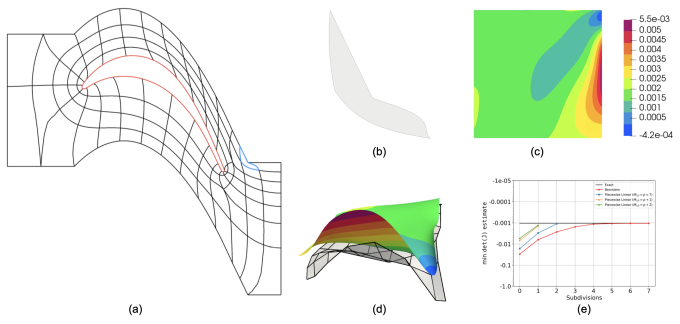
- Guaranteeing mesh validity: A novel bounding-approach is used to compute bounds on the determinant of the Jacobian of the transformation for each high-order element. These bounds are then used to guarantee positivity of Jacobian determinant everywhere in the mesh.
- PDE-constrained r-adaptivity: Node movement is used to simultaneously improve mesh quality and solution accuracy. The implicit dependence of the solution on the mesh nodes is captured via adjoint sensitivity analysis.
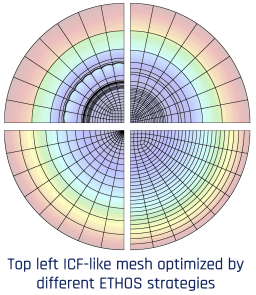
- TMOP-based adaptivity has been used for a wide variety of applications ranging from inertial confinement fusion, where symmetry preservation is important, to tokamak magnetohydrodynamics, where mesh alignment with the magnetic fields helps accelerate the convergence of the solution.
- The ETHOS algorithms are freely available on the MFEM website.
Team
- Vladimir Tomov (LLNL)
- Patrick Knupp (Dihedral, LLC)
- Tzanio Kolev (LLNL) – Project Leader
- Veselin Dobrev (LLNL)
- Ketan Mittal (LLNL)
Software
- Many of the high-order mesh optimization algorithms developed in the ETHOS project are freely available in a user-friendly form in the MFEM finite element library.
- See in particular the Mesh Optimizer miniapp in the miniapps/meshing directory and the TMOP sources in the fem directory.
Publications
- T. Kolev, B. Lazarov, K. Mittal, M. Schmidt, and V. Tomov, PDE-Constrained High-Order Mesh Optimization, Engineering with Computers.
- T. Dzanic, T. Kolev, and K. Mittal, A method for bounding high-order finite element functions: Applications to mesh validity and bounds-preserving limiters, Journal of Computational Physics, 545, (2026).
- K. Mittal, A. Parik, S. Dutta, P. Fischer, T. Kolev, and J. Lottes, General Field Evaluation in High-Order Meshes on GPUs, Computers & Fluids, 106606, (2025).
- K. Mittal, J.-L. Barrera, T. Kolev, M. Schmidt, and V. Tomov, High-Order Mesh hr-Adaptivity for Surface Fitting to Implicit Geometries. Lecture Notes in Computational Science and Engineering, (2025).
- V. Dobrev, P. Knupp, T. Kolev, K. Mittal, R. Rieben, M. Stees, and V. Tomov, Asymptotic Analysis of Compound Volume+ShapeMetrics for Mesh Optimization. International Meshing Roundtable, (2024).
- K. Mittal, V. Dobrev, P. Knupp, T. Kolev, F. Ledoux, C. Roche, and V. Tomov, Mixed-Order Meshes through Rp-Adaptivity for Surface Fitting to Implicit Geometries. International Meshing Roundtable, (2024).
- J.-L. Barrera, Tz. Kolev, K. Mittal, and V. Tomov, High-Order Mesh Morphing for Boundary and Interface Fitting to Implicit Geometries. Computer-Aided Design, 158, (2023).
- P. Knupp, Seventeen criteria for evaluating Jacobian-based optimization metrics. Engineering With Computers, (2023).
- J-S. Camier, V. Dobrev, P. Knupp, Tz. Kolev, K. Mittal, R. Rieben, and V. Tomov, Accelerating high-order mesh optimization using finite element partial assembly on GPUs. Journal of Computational Physics, 474, (2023).
- P. Knupp, Worst case mesh quality in the target matrix optimization paradigm. Engineering with Computers, 38(6), (2022).
- P. Knupp, Geometric parameters in the target matrix mesh optimization paradigm. Partial Differential Equations in Applied Mathematics, 100390, (2022).
- V. Dobrev, P. Knupp, Tz. Kolev, K. Mittal, and V. Tomov. hr-Adaptivity for nonconforming high-order meshes with the target matrix optimization paradigm. Engineering with Computers, 38(4), 3721-3737, (2022).
- P. Knupp, Tz. Kolev, K. Mittal, V. Tomov, Adaptive Surface Fitting and Tangential Relaxation for High-Order Mesh Optimization. International Meshing Roundtable, (2021).
- V. Dobrev, P. Knupp, Tz. Kolev, K. Mittal, V. Tomov, hr-adaptivity for nonconforming high-order meshes with the target-matrix optimization paradigm. Engineering with Computers, (2021).
- P. Knupp, Metric Type in the Target-matrix Mesh Optimization Paradigm (No. LLNL-TR-817490). Lawrence Livermore National Laboratory, Livermore, CA (2020).
- V. Dobrev, P. Knupp, Tz. Kolev, K. Mittal, R. Rieben, and V. Tomov, Simulation-Driven Optimization of High-Order Meshes in ALE Hydrodynamics. Computers & Fluids, 104602, (2020).
- P. Knupp, Target formulation and construction in mesh quality improvement (No. LLNL-TR-795097). Lawrence Livermore National Laboratory, Livermore, CA, (2019).
- V. Dobrev, P. Knupp, Tz. Kolev, and V. Tomov, Towards Simulation-Driven Optimization of High-Order Meshes by the Target-Matrix Optimization Paradigm, In International Meshing Roundtable (pp. 285-302). Springer, Cham (2019).
- V. Dobrev, P. Knupp, Tz. Kolev, K. Mittal, and V. Tomov, The Target-Matrix Optimization Paradigm for High-Order Meshes, SIAM J. Sci. Comput., 41(1), pp. B50–B68, (2019).
- R. Anderson, V. Dobrev, Tz. Kolev, R. Rieben, and V. Tomov, High-Order Multi-Material ALE Hydrodynamics, SIAM J. Sci. Comp., Vol. 40(1), pp. B32–B58, (2018).
- P. Knupp, Introducing the target-matrix paradigm for mesh optimization by node movement, Engineering with Computers 28(4), pp. 419–429, (2012).
Presentations
- MFEM Workshop 2025
- IMR 2025
- SIAM CSE 2025
- IMR 2024
- Tetrahedron 2023
- ICOSAHOM 2023
- NAHOMCon 2022
- IMR 2022
- IMR 2021
- ICOSAHOM 2021
- WCCM 2021
- MultiMat 2019
- SIAM CSE 2019
- SIAM CSE 2019
- ASCR 2019 PI poster
- ASCR 2018 PI poster
Gallery
- High-order mesh validity is determined by computing the lower bound on the determinant of the Jacobian of the transformation. [paper]
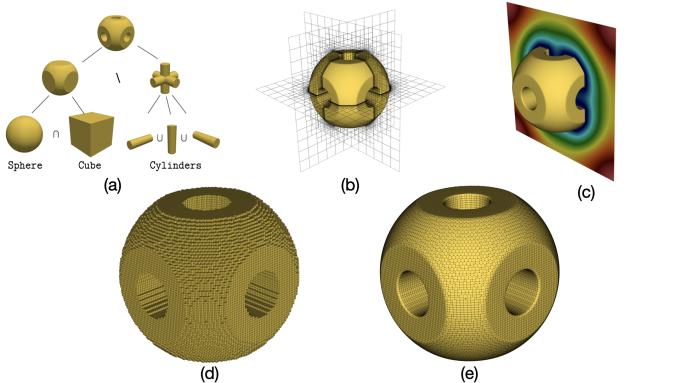
- Mixed-order mesh obtained through rp-adaptivity for fitting to implicit geometry. [paper]
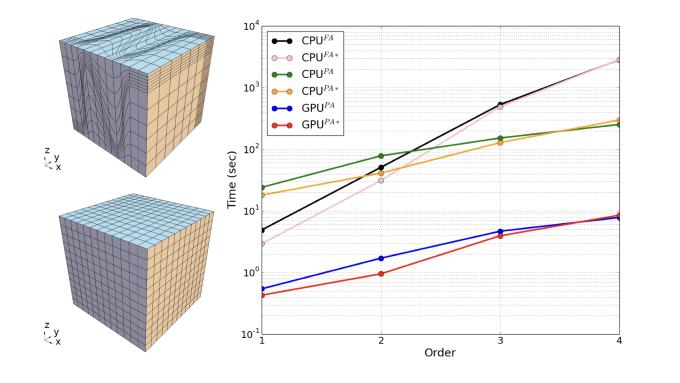
- Benchmark featuring Kershaw meshes shows that finite element partial assembly on GPUs leads to significant speed-up (30-40x) in comparison to full assembly on CPUs. [paper]
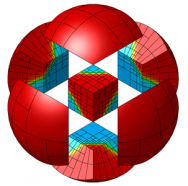
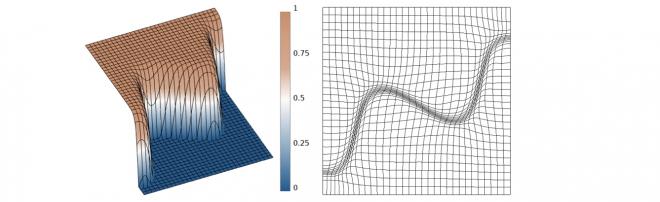
- Boundary and interface alignment to surfaces prescribed as the zero level-set of a discrete function [paper1, paper2].
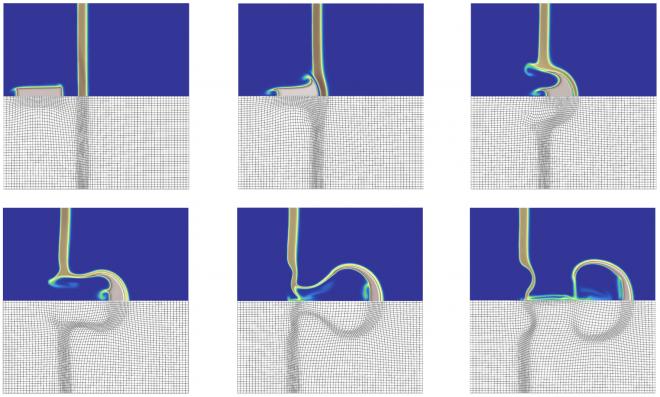
- Simulation-driven r-adaptivity [paper]
- Comparison of a mesh obtained from multi-material ALE hydrodynamics calculation in Laghos with r-adaptivity and hr-adaptivity meshes. [paper]
- Some fun mesh optimization using images. The meshes shown below are colored by element sizes.